已知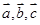 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 .
.
(1)若 ,且
,且 ,求:
,求: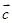 的坐标
的坐标
(2)若 ,且
,且 与
与 垂直,求
垂直,求 与
与 的夹角.
的夹角.
已知存在实数 和
和 使得
使得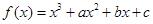
 .
.
(1)若 ,求
,求 的值;
的值;
(2)当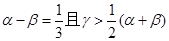 时,若存在实数
时,若存在实数 使得
使得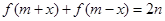 对任意
对任意 恒成立,求
恒成立,求 的最值.
的最值.
已知直线 被圆
被圆 截得的弦长恰与椭圆
截得的弦长恰与椭圆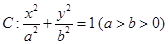 的短轴长相等,椭圆
的短轴长相等,椭圆 的离心率
的离心率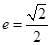 .
.
(1)求椭圆 的方程;
的方程;
(2)已知过点 的动直线
的动直线 交椭圆
交椭圆 于
于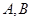 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点 ,使得无论
,使得无论 如何转动,以
如何转动,以 为直径的圆恒过定点
为直径的圆恒过定点 ?若存在,求出点
?若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
我国政府对PM2.5采用如下标准:
| PM2.5日均值m(微克/立方米) |
空气质量等级 |
 |
一级 |
 |
二级 |
 |
超标 |
某市环保局从一年365天的市区PM2.5监测数据中,随机抽取10天的数据作为样本,监测值如茎叶图所
示(十位为茎,个位为叶).
| 树茎 |
树叶 |
 2 2 |
8 2 |
| 3 |
8 2 1 |
| 4 |
4 5 |
| 6 |
3 8 |
| 7 |
7 |
(1)求这10天数据的中位数;
(2)从这10天数据中任取4天的数据,记 为空气质量达到一级的天数,求
为空气质量达到一级的天数,求 的分布列和期望;
的分布列和期望;
(3)以这10天的数据来估计这一年365天的空气质量情况,并假定每天之间的空气质量相互不影响.记 为这一年中空气质量达到一级的天数,求
为这一年中空气质量达到一级的天数,求 的平均值.
的平均值.
已知数列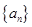 的前n项和为
的前n项和为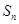 ,且
,且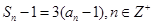 .
.
(1)求出数列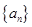 的通项公式;
的通项公式;
(2)设数列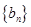 满足
满足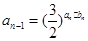 ,若
,若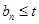 对于任意正整数n都成立,求实数t的取值范围.
对于任意正整数n都成立,求实数t的取值范围.
已知函数 .
.
(1)解不等式: ;
;
(2)已知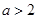 ,求证:
,求证: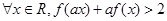 恒成立.
恒成立.