(本小题满分13分)
已知抛物线 (
(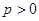 )上一点
)上一点 到其准线的距离为
到其准线的距离为 .
.
(Ⅰ)求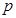 与
与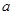 的值;
的值;
(Ⅱ)设抛物线 上动点
上动点 的横坐标为
的横坐标为 (
(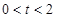 ),过点
),过点 的直线交
的直线交 于另一点
于另一点 ,交
,交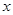 轴于
轴于 点(直线
点(直线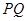 的斜率记作
的斜率记作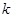 ).过点
).过点 作
作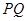 的垂线交
的垂线交 于另一点
于另一点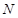 .若
.若 恰好是
恰好是 的切线,问
的切线,问 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.
设 且
且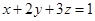
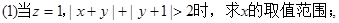
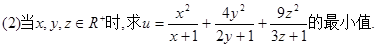
已知点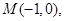 直线
直线 与曲线
与曲线
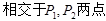 ,
,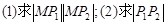
袋子里有完全相同的3只红球和4只黑球,今从袋子里随机取球.
(Ⅰ)若有放回地取3次,每次取一个球,求取出2个红球1个黑球的概率;
(Ⅱ)若无放回地取3次,每次取一个球,若取出每只红球得2分,取出每只黑球得1分,求得分 的分布列和数学期望.
的分布列和数学期望.
已知函数 f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.
(1)当a=-1时,求 的最大值;
的最大值;
(2)若f(x)在区间(0,e]上的最大值为-3,求a的值;
(3)当a=-1时,试推断方程 是否有实数解 .
是否有实数解 .
已知函数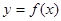 是定义域为
是定义域为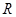 的奇函数,且当
的奇函数,且当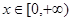 时,
时,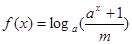 ,(
,( 。
。
(1)求实数 的值;并求函数
的值;并求函数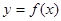 在定义域
在定义域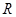 上的解析式;
上的解析式;
(2)求证:函数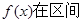
 上是增函数。
上是增函数。