(本小题满分13分)
某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
| 日期 |
3月1日 |
3月2日 |
3月3日 |
3月4日 |
3月5日 |
| 温差x(oC) |
10 |
11 |
13 |
12 |
8 |
| 发芽数y(颗) |
23 |
25 |
30 |
26 |
16 |
(I)从3月1日至3月5日中任选2天,记发芽的种子数分别为m,n,求事件“m,n均小于25”的概率;
(II)请根据3月2日至3月4日的数据,求出y关于x的线性回归方程 ;
;
(III)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(II)所得的线性回归方程是否可靠?
(参考公式:回归直线方程式 ,其中
,其中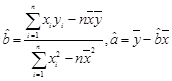 )
)
(本小题满分12分)如图,已知在直三棱柱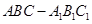 中,
中, 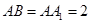 ,
,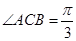 ,点D是线段
,点D是线段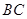 的中点.
的中点.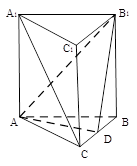
(Ⅰ)求证: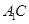 ∥平面
∥平面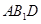 ;
;
(Ⅱ)当三棱柱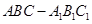 的体积最大时,求直线
的体积最大时,求直线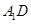 与平面
与平面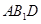 所成角
所成角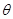 的正弦值.
的正弦值.
某校男女篮球队各有10名队员,现将这20名队员的身高绘制成如下茎叶图(单位:cm).男队员身高在180cm以上定义为“高个子”,女队员身高在170cm以上定义为“高个子”,其他队员定义为“非高个子”.用分层抽样的方法,从“高个子”和“非高个子”中共抽取5名队员.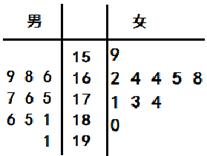
(Ⅰ)从这5名队员中随机选出2名队员,求这2名队员中有“高个子”的概率;
(Ⅱ)求这5名队员中,恰好男女“高个子”各1名队员的概率.
(本小题满分12分)已知函数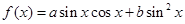 ,
,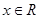 ,且
,且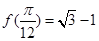 ,
,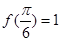 .
.
(Ⅰ)求函数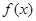 的单调递增区间;
的单调递增区间;
(Ⅱ)若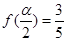 ,
,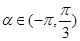 ,求
,求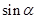 的值.
的值.
(本小题满分10分)选修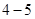 :不等式选讲
:不等式选讲
已知函数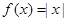 ,
,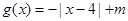
(Ⅰ)解关于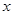 的不等式
的不等式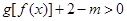 ;
;
(Ⅱ)若函数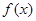 的图像恒在函数
的图像恒在函数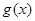 图像的上方,求实数
图像的上方,求实数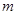 的取值范围.
的取值范围.
(本小题满分10分)选修 ;坐标系与参数方程
;坐标系与参数方程
在直角坐标系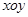 中,以坐标原点为极点,
中,以坐标原点为极点,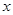 轴正半轴为极轴建立极坐标系,已知某圆的极坐标方程为:
轴正半轴为极轴建立极坐标系,已知某圆的极坐标方程为: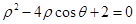 .
.
(Ⅰ)将极坐标方程化为普通方程;
(Ⅱ)若点P(x,y)在该圆上,求x+y的最大值和最小值.