如图,已知椭圆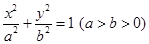 的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为
,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为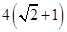 。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。
。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。
(1)求椭圆和双曲线的标准方程
(2)设直线PF1、PF2的斜率分别为k1、k2,证明:k1·k2=1
(3)是否存在常数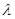 ,使得|AB|+|CD|=
,使得|AB|+|CD|=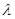 |AB|·|CD|恒成立?
|AB|·|CD|恒成立?
若存在,求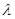 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(本小题满分12分) 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图4.( )
)
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
(本小题满分12分)已知函数 (其中
(其中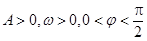 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为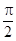 ,且图象上一个最低点为
,且图象上一个最低点为 .
.
(1)求 的解析式;
的解析式;
(2)当 ,求
,求 的值域.
的值域.
.如图,四边形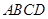 为矩形,
为矩形,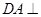 平面
平面 ,
, ,
, 平面
平面 于点
于点 ,且点
,且点 在
在 上.
上.
(1)求证: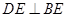 ;(2)求四棱锥
;(2)求四棱锥 的体积;
的体积;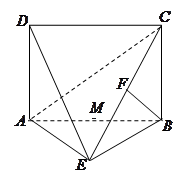
(3)设点 在线段
在线段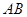 上,且
上,且 ,试在线段
,试在线段 上确定一点
上确定一点 ,使得
,使得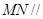 平面
平面 .
.
数列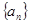 的前n项和为
的前n项和为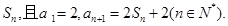
(1)求数列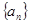 的通项公式;
的通项公式;
(2)等差数列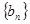 的各项为正,其前n项和为
的各项为正,其前n项和为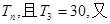
 成等比数列,求
成等比数列,求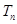 的最小值.
的最小值.
在 中,已知
中,已知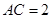 ,
, ,
,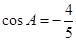 .
.
(1)求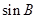 的值;(2)求
的值;(2)求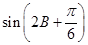 的值.
的值.