已知椭圆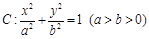 的离心率为
的离心率为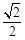 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线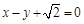 相切.
相切.
(Ⅰ)求椭圆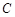 的方程;
的方程;
(Ⅱ)若过点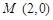 的直线与椭圆
的直线与椭圆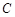 相交于两点
相交于两点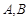 ,设
,设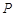 为椭圆上一点,且满足
为椭圆上一点,且满足 (
(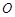 为坐标原点),当
为坐标原点),当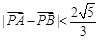 时,求实数
时,求实数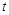 的取值范围.
的取值范围.
(本题满分16分,第(1)小题6分,第(2)小题10分)
为了让更多的人参与2010年在上海举办的“世博会”,上海某旅游公司面向国内外发行总量为2000万张的旅游优惠卡,其中向境外人士发行的是世博金卡(简称金卡),向境内人士发行的是世博银卡(简称银卡)。现有一个由36名游客组成的旅游团到上海参观旅游,其中 是境外游客,其余是境内游客。在境外游客中有
是境外游客,其余是境内游客。在境外游客中有 持金卡,在境内游客中有
持金卡,在境内游客中有 持银卡。.
持银卡。. 


(1)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率;
(2)在该团的境内游客中随机采访3名游客,设其中持银卡人数为随机变量 ,求
,求 的分布列及数学期望
的分布列及数学期望 。
。
(本题满分14分,第(1)小题4分,第(2)小题4分,第(2)小题6分)
设数列 中,若
中,若 ,则称数列
,则称数列 为“凸数列”。
为“凸数列”。
(1)设数列 为“凸数列”,若
为“凸数列”,若 ,试写出该数列的前6项,并求出该6项之和;
,试写出该数列的前6项,并求出该6项之和;
(2)在“凸数列” 中,求证:
中,求证: ;
;
(3)设 ,若数列
,若数列 为“凸数列”,求数列前
为“凸数列”,求数列前 项和
项和 。
。
(本题满分14分,第(1)小题6分,第(2)小题8分) 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD= ,点E是线段SD上任意一点。
,点E是线段SD上任意一点。
(1)求证:AC⊥BE;
(2)若二面角C-AE-D的大小为 ,求线段
,求线段 的
的 长。
长。
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
在数列 中,
中, ,
, .
.
(1)设
 ,证明:数列
,证明:数列 是等差数列;
是等差数列;
(2)设 数列
数列 的前
的前 项和为
项和为 ,求
,求 的值;
的值;
(3)设 ,数列
,数列 的前
的前 项和为
项和为 ,
, ,是否存在
,是否存在 实数
实数 ,使得对任意的正整数
,使得对任意的正整数 和实数
和实数 ,都有
,都有 成立?请说明理由.
成立?请说明理由.
本题共有3个小题,第1小题满分4分,第2小题满分6分、第3小题满分6分.
已知 的顶点
的顶点 在椭圆
在椭圆 上,
上, 在直线
在直线 上,
上,
且 .
.
(1)求边 中点的轨迹方程;
中点的轨迹方程;
(2)当 边通过坐标原点
边通过坐标原点 时,求
时,求 的面积;
的面积;
(3)当 ,且斜边
,且斜边 的长最大时,求
的长最大时,求 所在直线的方程.
所在直线的方程.