某学校今年为山区捐款28000元,比去年的2倍还多500元,去年该学校为山区捐款多少元?
OM是∠AOB的平分线,射线OC在∠BOM内,ON是∠BOC的平分线,已知∠AOC=80º,那么∠MON的度数是多少?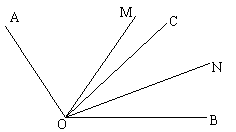
如图,OC是∠AOD的平分线,OE是∠BOD的平分线。(1)如果∠AOB=130°,那么∠COE是多少度? (2)如果∠COE=65°,∠COD=20°,那么∠BOE是多少度?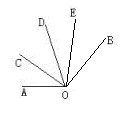
如图,直线AB上一点O,OM、ON分别是∠AOC、∠BOC的平分线。求:∠MON的度数。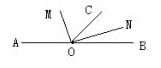
直线AB、CD交于点O,且∠BOC =80°,OE平分∠BOC,OF为OE的反向延长线,求:1)∠2和∠3的度数。 2)OF平分∠AOD吗?