如图,在 中, , ,点 在边 上,且 , ,垂足为点 ,联结 ,求:
(1)线段 的长;
(2) 的余切值.

解方程:
(1)2(x+2)2 -8=0
(2)
如图,抛物线 交x轴于A,B两点(A在B左侧),交y轴于点C.已知一次函数y=kx+b的图象过点A,C.
交x轴于A,B两点(A在B左侧),交y轴于点C.已知一次函数y=kx+b的图象过点A,C.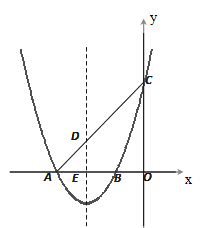
(1)求抛物线的对称轴和一次函数的解析式;
(2)根据图象,写出满足kx+b>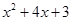 的x的取值范围;
的x的取值范围;
(3)在平面直角坐标系xoy 中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由.
某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加x元.求:
(1)房间每天的入住量y(间)关于x(元)的函数关系式;
(2)该宾馆每天的房间收费z(元)关于x(元)的函数关系式;
(3)该宾馆客房部每天的利润w(元)关于x(元)的函数关系式;当每个房间的定价为每天多少元时,w有最大值?最大值是多少?
如图,已知AB为⊙O的直径,CD是弦,且AB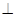 CD于点E.连接AC、OC、BC.
CD于点E.连接AC、OC、BC.
(1)求证: ACO=
ACO= BCD;
BCD;
(2)若AE=18cm,CD=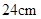 ,求⊙O的面积.
,求⊙O的面积.
如图,有一面积是150平方米的长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米, 求鸡场的长和宽各为多少米.