如图所示,一段街道的两边缘所在直线分别为AB、PQ,并且AB∥PQ.建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N.小亮从胜利街的A处,沿着AB方向前进,小明一直站在点P的位置等候小亮.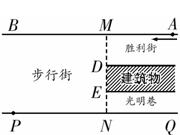
(1)请你在图中画出小亮恰好能看见小明时的视线,以及此时小亮所在位置(用点C标出);
(2)已知:MN=20m,MD=8m,PN=24m,求(1)中的点C到胜利街口的距离CM.
化简: .
.
已知二次函数 (a>0)的图象与x轴交于A(x1,0)、B(x2,0)(x1<x2)两点,与y轴交于点C,x1,x2是方程
(a>0)的图象与x轴交于A(x1,0)、B(x2,0)(x1<x2)两点,与y轴交于点C,x1,x2是方程 的两根.
的两根.
(1)若抛物线的顶点为D,求S△ABC:S△ACD的值;
(2)若∠ADC=90°,求二次函数的解析式.
如图,在等边△ABC中,AB=3,D、E分别是AB、AC上的点,且DE∥BC,将△ADE沿DE翻折,与梯形BCED重叠的部分记作图形L.
(1)求△ABC的面积;
(2)设AD=x,图形L的面积为y,求y关于x的函数解析式;
(3)已知图形L的顶点均在⊙O上,当图形L的面积最大时,求⊙O的面积.
如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC.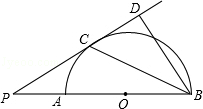
(1)求证:BC平分∠PDB;
(2)求证:BC2=AB•BD;
(3)若PA=6,PC=6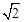 ,求BD的长.
,求BD的长.
某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在30≤x≤120,具有一次函数的关系,如下表所示.
| x |
50 |
60 |
90 |
120 |
| y |
40 |
38 |
32 |
26 |
(1)求y关于x的函数解析式;
(2)后来在修建的过程中计划发生改变,政府决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.