为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限高,请你根据该图计算CE.(精确到0.1m)
(下列数据提供参考: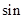 20°=0.3420,
20°=0.3420, 20°=0.9397,
20°=0.9397,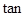 20°=0.3640)
20°=0.3640) 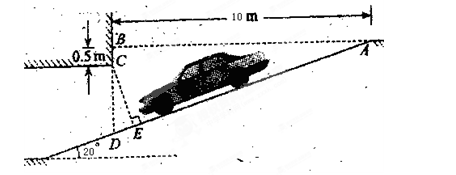
(本题满分12分 第(1)小题6分,第(2)小题6分)
已知:如图,二次函数 x2
x2  x
x  的图像与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为Q,直线QB与y轴交于点E.
的图像与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为Q,直线QB与y轴交于点E.
(1)求点E的坐标;
(2)在x轴上方找一点C,使以点C、O、B为顶点的三角形与△BOE相似,请直接写出点C的坐标.
(本题满分12分 第(1)小题6分,第(2)小题6分)
已知:如图,在△ABC中,BD⊥AC于点D, CE⊥AB于点E,EC和BD相交于点O,联接DE. 
(1)求证:△EOD∽△BOC;
(2)若S△EOD=16,S△BOC=36,求 的值.
的值.
已知:如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点M、N分别在边AO和边OD上,且AM= AO,ON=
AO,ON= OD,设
OD,设 =
= ,
, =
= ,试用
,试用 、
、 的线性组合表示向量
的线性组合表示向量 和向量
和向量 .
.
已知:如图六,九年级某班同学要测量校园内旗杆CH的高度,在地面的点E处用测角器测得旗杆顶点C的仰角∠CAD=45°,再沿直线EF向着旗杆方向行走10米到点F处,在点F又用测角器测得旗杆顶点C的仰角∠CBA=60°;已知测角器的高度为1.6米,求旗杆CH的高度(结果保留根号).
(本题满分10分 第(1)小题4分,第(2)小题6分)
已知:二次函数 ≠0的图像经过点(3,5)、(2,8)、(0,8).
≠0的图像经过点(3,5)、(2,8)、(0,8).
(1)求这个二次函数的解析式;
(2)已知抛物线 ≠0,
≠0, ≠0,且满足
≠0,且满足 ≠0,1,则我们称抛物线
≠0,1,则我们称抛物线 互为“友好抛物线”,请写出当
互为“友好抛物线”,请写出当 时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.
时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.