题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.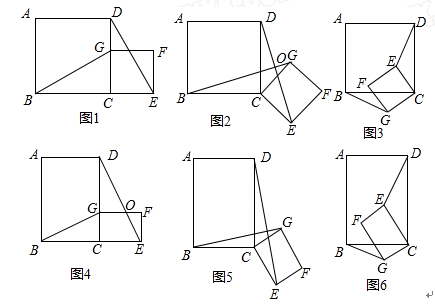
问题探究:(1)①如图1所示,当G在CD边上时,猜想线段BG、DE的数量关系及所在直线的位置关系.(不要求证明)
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2,如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,请选择图2或图3证明你的判断.
类比研究:(2)若将原题中的“正方形”改为“矩形”(如图所示),且
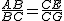 =k(其中k>0),请写出 线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断(仅证数量关系).
=k(其中k>0),请写出 线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断(仅证数量关系).
拓展应用:(3)在(1)中图2中,连接DG、BE,若AB=3,EF=2,求BE2+DG2的值.
某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图.根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)求扇形统计图中m的值和“E”组对应的圆心角度数;
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数.
解方程:  =
= 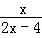 ﹣1.
﹣1.
化简:( +
+ )÷
)÷  .
.
(1)有甲、乙、丙三种商品,如果购甲3件、乙2件、丙1件共需15元,如果购甲1件、乙2件、丙3件共需25元,那么购甲、乙、丙各1件共需多少元?
(2)已知2a+b+3c=15,3a+b+5c=25,则a+b+c=
(3)已知2a+b+xc=15,3a+b+yc=25, 要想求出a+b+c的值,x与y必须满足的关系是?
(10分)如图,四边形 中,
中, ,
, 平分
平分 交
交 于
于 ,
, 平分
平分 交
交 于
于 .
.
(1)若 ,则
,则 °,
°, °;
°;
(2)求证:BE∥DF