(1)有甲、乙、丙三种商品,如果购甲3件、乙2件、丙1件共需15元,如果购甲1件、乙2件、丙3件共需25元,那么购甲、乙、丙各1件共需多少元?
(2)已知2a+b+3c=15,3a+b+5c=25,则a+b+c=
(3)已知2a+b+xc=15,3a+b+yc=25, 要想求出a+b+c的值,x与y必须满足的关系是?
在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
(1)如图,当C点在x轴上运动时,设AC=x,请用x表示线段AD的长;
(2)随着C点的变化,直线AE的位置变化吗?若变化,请说明理由;若不变,请求出直线AE的解析式.
(3)以线段BC为直径作圆,圆心为点F,
①当C点运动到何处时直线EF∥直线BO?此时⊙F和直线BO的位置关系如何?请说明理由.
②G为CD与⊙F的交点,H为直线DF上的一个动点,连结HG、HC,求HG+HC的最小值,并将此最小值用x表示.
已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.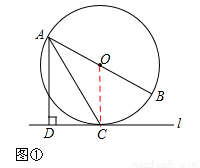
(1)如图①,当直线l与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
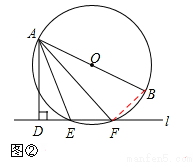
(2)如图②,当直线l与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
已知:如图,AB是⊙O的直径,AC是⊙O的弦,AB=2,∠BAC=300.在图中作弦AD,使AD=1,并求∠CAD的度数。
已知Rt△ABC,.∠A=900求作一个圆,使圆心O在AC上,且与AB、BC所在的直线相切(不写作法,保留作图痕迹,并说明作图的理由)。
某校学生会向全校1900名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为________,图①中m的值是________;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.