设 的内角
的内角 的对边分别为
的对边分别为 .已知
.已知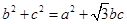 ,求:
,求:
(Ⅰ)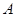 的大小;
的大小;
(Ⅱ)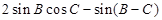 的值.
的值.
已知 的顶点
的顶点 、
、 、
、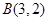 ,
, 边上的中线所在直线为
边上的中线所在直线为 .
.
(Ⅰ)求 的方程;
的方程;
(Ⅱ)求点 关于直线
关于直线 的对称点的坐标.
的对称点的坐标.
如图,已知四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=DC, 点E是PC的中点,作 交PB于点F.
交PB于点F.
(1)求证:PB⊥平面EFD;
(2)求二面角C-PB-D的大小.
已知圆C: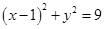 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线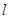 交圆C于A、B两点.
交圆C于A、B两点.
(1)当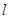 经过圆心C时,求直线l的方程;
经过圆心C时,求直线l的方程;
(2)当弦AB最短时,写出直线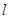 的方程;
的方程;
(3)当直线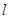 的倾斜角为45º时,求弦AB的长.
的倾斜角为45º时,求弦AB的长.
如图1,在Rt△ABC中,∠C=90°,BC=6,AC=3,D,E分别是AC,AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(1)求证: 平面
平面 ;
;
(2)过点E作截面
 平面
平面 ,分别交CB于F,
,分别交CB于F, 于H,求截面
于H,求截面 的面积。
的面积。
已知两直线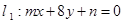 和
和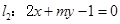 .试确定
.试确定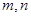 的值,使
的值,使
(1)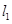 与
与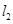 相交于点
相交于点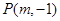 ;
;
(2)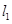 ∥
∥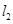 ;
;
(3)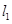
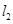 ,且
,且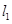 在
在 轴上的截距为-1.
轴上的截距为-1.