设函数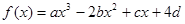
（a、b、c、d∈R）图象C关于原点对称，且x=1时，
取极小值
（1）求f(x)的解析式；
（2）当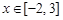
时,求函数f(x)的最大值.
（本小题满分12分）已知等差数列
的首项
，前n项和为Sn，且
成等差数列．
（1）求数列
的通项公式；
（2）若数列{bn}为递增的等比数列，且集合
，设数列
的前n项和为
，求．
（本小题满分12分）设数列
的首项为1，前n项和为Sn，且
（
）．
（1）求数列
的通项公式；
（2）设
，
是数列
的前n项和，求
．
（本小题满分12分）在直三棱柱
中，
，
， 异面直线
与
所成的角等于
，设
．
（1）求a的值；
（2）求平面
与平面
所成的锐二面角的大小．
（本小题满分12分）已知a，b，c分别是△ABC的三个内角A，B，C所对的边，且
．
（1）求角C的值；
（2）若
，△ABC的面积
，求a的值．
设函数
，
（Ⅰ）讨论函数
的单调性
（Ⅱ）如果存在
，使得
成立，求满足上述条件的最大整数
（Ⅲ）如果对任意的
，都有
成立，求实数
的取值范围