命题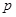 :函数
:函数 的定义域为
的定义域为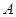 ,
,
命题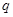 :
: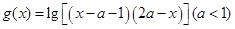 的定义域为
的定义域为 ,若
,若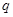 是
是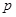 的充分条件,求实数
的充分条件,求实数 的取值范围。
的取值范围。
已知,椭圆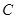 经过点
经过点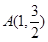 ,两个焦点的坐标为
,两个焦点的坐标为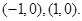
(Ⅰ)求椭圆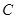 的方程;(Ⅱ)
的方程;(Ⅱ) 是椭圆
是椭圆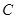 上的两个动点,如果直线
上的两个动点,如果直线 的斜率与
的斜率与 的斜率互为相反数,证明:直线
的斜率互为相反数,证明:直线 的斜率为定值,并求出这个定值。
的斜率为定值,并求出这个定值。
(1)证明直线和平面垂直的判定定理,即已知:如图1,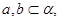 且
且 ,
, 求证:
求证:
(2)请用直线和平面垂直的判定定理证明:如果一条直线垂直于两个平行平面中的一个,那么它也垂直于另一个平面,即
已知:如图2,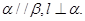 求证:
求证:
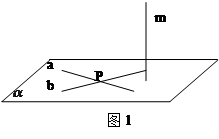
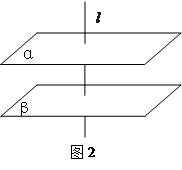
已知中心在原点,对称轴为坐标轴的双曲线的一个焦点为
且该双曲线上一点到两个焦点的距离差的绝对值为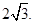
(Ⅰ)求双曲线的标准方程.
(Ⅱ)过点 且倾斜角为
且倾斜角为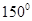 的直线与双曲线交于
的直线与双曲线交于 两点,求线段
两点,求线段 的长。
的长。
如图,在正三棱柱 中,
中, 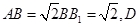 为
为 的中点。
的中点。
(Ⅰ)求证: 平面
平面 ;(Ⅱ)求直线
;(Ⅱ)求直线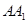 与平面
与平面 所成角的正弦值
所成角的正弦值
如图,在四棱锥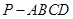 中,底面
中,底面 为正方形,侧棱
为正方形,侧棱 底面
底面 ,
, ,点
,点 为
为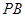 的中点。
的中点。
(Ⅰ)求证: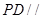 平面
平面 ;
;
(Ⅱ)求点 到平面
到平面 的距离。
的距离。