提出问题：如图，有一块分布均匀的等腰三角形蛋糕（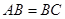
，且
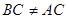），在蛋糕的边缘均匀分布着巧克力，小明和小华决定只切一刀将这块蛋糕平分（要求分得的蛋糕和巧克力质量都一样）．
背景介绍：这条分割直线即平分了三角形的面积，又平分了三角形的周长，我们称这条线为三角 形的“等分积周线”．
尝试解决：
（1）小明很快就想到了一条分割直线，而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”，从而平分蛋糕．
（2） 小华觉得小明的方法很好，所以自己模仿着在图1中过点C画了一条直线CD交AB于点D．你觉得小华会成功吗？如能成功，说出确定的方法；如不能成功，请说明理由．
（3）通过上面的实践，你一定有了更深刻的认识．请你解决下面的问题：若AB＝BC＝5 cm，AC＝6 cm，请你找出△ABC的所有“等分积周线”，并简要的说明确定的方法．
如图（1），某建筑物有一抛物线形的大门，小强想知道这道门的高度. 他先测出门的宽度
，然后用一根长为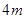
的小竹杆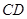
竖直地接触地面和门的内壁，并测得
. 小强画出了如图（2）的草图，请你帮他算一算门的高度
.
要测量一个钢板上的小孔的直径，通常采用间接的测量方法．如果用一个直径为10mm的标准钢珠放在小孔上，测的钢珠顶端与小孔平面的距离h="8" mm（如图），求此小孔的直径d．
果园有100棵桃树，一棵桃树平均结1000个桃子，现准备多种一些桃树以提高产量，试验发现，每多种一棵桃树，每棵树的产量就会减少2个，多种的桃树不能超过100棵，如果要使产量增加15.2%，那么应多种多少棵桃树？
请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题，并进行证明：
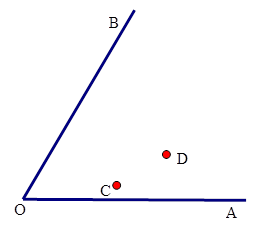
如图，求作一点P，使PC=PD，并且点P到∠AOB两边的距离相等（不写作法，但保留作图痕迹）