已知焦点在X轴上的椭圆C为. ,F1、F2分别是椭圆C的左、右焦点,离心率e=
,F1、F2分别是椭圆C的左、右焦点,离心率e=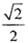 .
.
(I )求椭圆C的方程;
(II) 设点Q的坐标为(1,0),椭圆上是否存在一点P,使得直线 都与以Q为圆心的一个圆相切,如存在,求出P点坐标及圆的方程,如不存在,请说明理由.
都与以Q为圆心的一个圆相切,如存在,求出P点坐标及圆的方程,如不存在,请说明理由.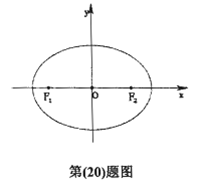
如图,在直三棱柱 中,D、E分别为
中,D、E分别为 、AD的中点,F为
、AD的中点,F为 上的点,且
上的点,且

(I)证明:EF∥平面ABC;
(Ⅱ)若 ,
, ,求二面角
,求二面角 的大小.
的大小.
(在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如下茎叶图所示:
(Ⅰ)从甲、乙两人中选择1人参加数学趣味知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(II)从乙的6次培训成绩中随机选择2个,记被抽到的分数超过115分的个数为 ,试求
,试求 的分布列和数学期望.
的分布列和数学期望.
已知等差数列 中,
中, ;
; 是
是 与
与 的等比中项.
的等比中项.
(I)求数列 的通项公式:
的通项公式:
(II)若 .求数列
.求数列 的前
的前 项和.
项和.
已知定义在 上的函数
上的函数 ,其中
,其中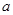 为常数.
为常数.
(1)当 是函数
是函数 的一个极值点,求
的一个极值点,求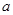 的值;
的值;
(2)若函数 在区间
在区间 上是增函数,求实数
上是增函数,求实数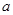 的取值范围;
的取值范围;
(3)当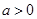 时,若
时,若 ,在
,在 处取得最大值,求实数
处取得最大值,求实数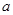 的取值范围.
的取值范围.
已知函数 .
.
(1)若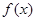 在
在 处取得极大值,求实数
处取得极大值,求实数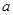 的值;
的值;
(2)若 ,求
,求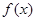 在区间
在区间 上的最大值.
上的最大值.