在长方体
中，
，
分别是所在棱
的中点，点
是棱
上的动点，联结
．如图所示．
（1）求异面直线
所成角的大小（用反三角函数值表示）；
（2）求以
为顶点的三棱锥的体积．
（本小题满分13分）已知函数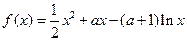
（
）．
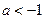（1）若函数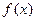
在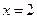
处的切线与x轴平行，求a的值，并求出函数的极值；
（2）已知函数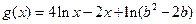
，在（1）的条件下，若
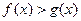恒成立，求b的取值范围．
（本小题满分12分）
设数列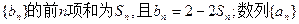
为等差数列，且a5=14，a7=20。
（1）求数列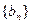
的通项公式；
（2）若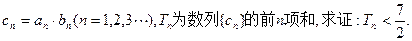
已知直线l经过抛物线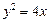
的焦点F，
且与抛物线相交于A、B两点.
（1）若
，求点A的坐标；
（2）若直线l的倾斜角为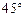
，求线段AB的长.
.(本小题满分12分)
在△ABC中，角A、B、C的对应边分别为a，b，c，且满足a2－ab＋b2＝c2.
(1)求角C；
(2)若△ABC的面积为，c＝2，求a＋b的值.
：已知矩阵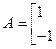
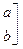,A的一个特征值
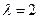，其对应的特征向量是
.
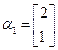（Ⅰ）求矩阵
；
（Ⅱ）求直线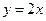
在矩阵M所对应的线性变换下的像的方程