(本题满分14分)
如图,已知四棱锥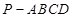 ,底面
,底面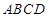 为菱形,
为菱形,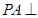 平面
平面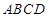 ,
,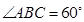 ,
,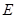 是
是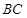 的中点,
的中点,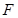 为线段
为线段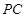 上一点.
上一点.
(Ⅰ)求证: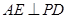 ;
;
(Ⅱ)若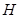 为
为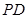 上的动点,
上的动点,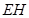 与平面
与平面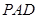 所成最大角的 正切值为
所成最大角的 正切值为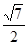 ,若二面角
,若二面角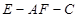 的余弦值为
的余弦值为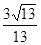 ,求
,求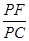 的值。
的值。
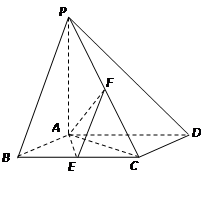
如图所示,在矩形ABCD中,AB=a,BC=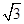 a,以对角线AC为折线将直角三角形ABC向上翻折到三角形APC的位置(B点与P点重合),P点在平面ACD上的射影恰好落在边AD上的H处.
a,以对角线AC为折线将直角三角形ABC向上翻折到三角形APC的位置(B点与P点重合),P点在平面ACD上的射影恰好落在边AD上的H处.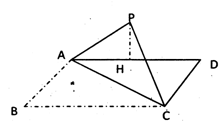
(1)求证:PA⊥CD;
(2)求直线PC与平面ACD所成角的正切值.
己知各项均不相等的等差数列{an}的前四项和S4=14,且a1,a3,a7成等比数列.
(1)求数列{an}的通项公式;
(2)设Tn为数列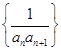 的前n项和,若Tn≤
的前n项和,若Tn≤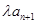 ¨对
¨对 恒成立,求实数
恒成立,求实数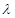 的最小值.
的最小值.
己知函数 在
在 处取最小值.
处取最小值.
(1)求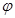 的值。
的值。
(2)在△ABC中,a、b、c分别是A、B、C的对边,已知a=l,b=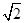 ,
, ,求角C.
,求角C.
已知函数y="Asin(ωx+φ)" (A>0,ω>0,|φ|<π)的 一段图象如图所示 
(1)求函数的解析式;
(2)求这个函数的单调增区间。
已知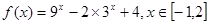
(1)设 ,求
,求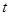 的最大值与最小值;
的最大值与最小值;
(2)求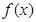 的最大值与最小值;
的最大值与最小值;