在彩色显影中,由经验可知:形成染料光学密度 与析出银的光学密度
与析出银的光学密度 由公式
由公式 表示,现测得试验数据如下:
表示,现测得试验数据如下:
 |
0.05 |
0.25 |
0.10 |
0.20 |
0.50 |
 |
0.10 |
1.00 |
0.37 |
0.79 |
1.30 |
(1)写出变换过程,并列出新变量的数据表;
(2)求出b与a ,并写出 对
对 的回归方程。(精确到0.01)
的回归方程。(精确到0.01)
(参考数据;Ln0.1 -2.30,Ln0.37
-2.30,Ln0.37 -0.10, Ln0.79
-0.10, Ln0.79 -0.24, Ln1.30
-0.24, Ln1.30 0.26,
0.26, ,
, ,
, )
)
(本小题共13分)
在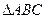 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为 、
、 、
、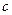 ,角A、B、C成等差数列,
,角A、B、C成等差数列,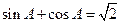 ,边
,边 的长为
的长为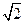 .
.
(I)求边 的长;
的长;
(II)求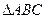 的面积.
的面积.
已知定义在实数集上的函数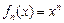 ,
,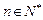 ,其导函数记为
,其导函数记为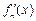 ,且满足:
,且满足:
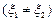 ,
,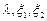 为常数.
为常数.
(Ⅰ)试求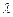 的值;
的值;
(Ⅱ)设函数 与
与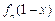 的乘积为函数
的乘积为函数 ,求
,求 的极大值与极小值;
的极大值与极小值;
(Ⅲ)试讨论关于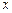 的方程
的方程 在区间
在区间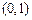 上的实数根的个数.
上的实数根的个数.
设MN是双曲线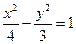 的弦,且MN与
的弦,且MN与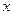 轴垂直,
轴垂直,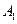 、
、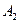 是双曲线的左、右顶点.
是双曲线的左、右顶点.
(Ⅰ)求直线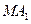 和
和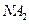 的交点的轨迹C的方程;
的交点的轨迹C的方程;
(Ⅱ) 设直线y=x-1与轨迹C交于A、B两点,若轨迹C上的点P满足
设直线y=x-1与轨迹C交于A、B两点,若轨迹C上的点P满足 (
(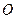 为坐标原点,
为坐标原点,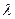 ,
,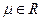 )
)
求证: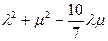 为定值,并求出这个定值.
为定值,并求出这个定值.
如图,在矩形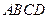 中,
中,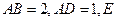 是
是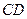 的中点,以
的中点,以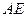 为折痕将
为折痕将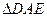 向上折起,使
向上折起,使 为
为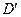 ,且平面
,且平面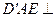 平面
平面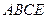 .
.
(Ⅰ)求证: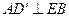 ;
;
(Ⅱ)求直线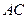 与平面
与平面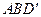 所成角的正弦值.
所成角的正弦值.
某工厂每月生产某种产品三件,经检测发现,工厂生产该产品的合格率为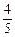 ,已知生产一件合格品能盈利25万元,生产一件次品将会亏损10万元,假设该产品任何两件之间合
,已知生产一件合格品能盈利25万元,生产一件次品将会亏损10万元,假设该产品任何两件之间合 格与否相互没有影响.
格与否相互没有影响.
(Ⅰ)求工厂每月盈利额ξ(万元)的所有可能取值;
(Ⅱ)若该工厂制定了每月盈利额不低于40万元的目标,求该工厂达到盈利目标的概率;
(Ⅲ)求工厂每月盈利额ξ的分布列和数学期望.