在直角坐标系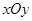 中,点
中,点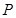 到两点
到两点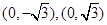 的距离之和为4,设点
的距离之和为4,设点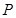 的轨迹为
的轨迹为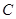 ,直线
,直线 与
与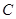 交于
交于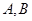 两点.
两点.
(1)写出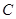 的方程;
的方程;
(2)若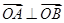 ,求
,求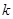 的值
的值
某一中学生心理咨询中心服务电话接通率为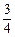 ,某班3名同学商定明天分别就同一问题询问服务中心,且每人只拨打一次,求他们中成功咨询的人数X的分布列.
,某班3名同学商定明天分别就同一问题询问服务中心,且每人只拨打一次,求他们中成功咨询的人数X的分布列.
如图,电路由电池 并联组成.电池
并联组成.电池 损坏的概率分别是0.3,0.2,0.2,求电路断电的概率.
损坏的概率分别是0.3,0.2,0.2,求电路断电的概率.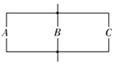
某种项目的射击比赛,开始时在距目标100m处射击,如果命中记3分,且停止射击;若第一次射击未命中,可以进行第二次射击,但目标已在150m处,这时命中记2分,且停止射击;若第二次仍未命中,还可以进行第三次射击,此时目标已在200m处,若第三次命中则记1分,并停止射击;若三次都未命中,则记0分.已知射手甲在100m处击中目标的概率为 ,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
(1)求这位射手在三次射击中命中目标的概率;
(2)求这位射手在这次射击比赛中得分的均值.
甲、乙、丙三名射击选手,各射击一次,击中目标的概率如下表所示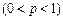 :
:
| 选手 |
甲 |
乙 |
丙 |
| 概率 |
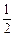 |
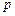 |
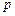 |
若三人各射击一次,恰有k名选手击中目标的概率记为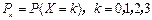 .
.
(1)求X的分布列;(2)若击中目标人数的均值是2,求P的值.
甲、乙两人独立地破译1个密码,他们能译出密码的概率分别为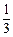 和
和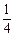 ,求
,求
(1)恰有1人译出密码的概率;
(2)若达到译出密码的概率为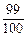 ,至少需要多少乙这样的人.
,至少需要多少乙这样的人.