一校办服装厂花费2万元购买某品牌运动装的生产与销售权.根据以往经验,每生产1百套这种品牌运动装的成本为1万元,每生产 (百套)的销售额
(百套)的销售额 (万元)满足:
(万元)满足:
(1)该服装厂生产750套此种品牌运动装可获得利润多少万元?
(2)该服装厂生产多少套此种品牌运动装利润最大?此时,利润是多少万元?
(本小题满分14分)(文科)已知曲线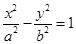
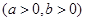 的离心率
的离心率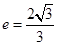 ,直线
,直线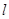 过
过 、
、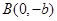 两点,原点
两点,原点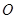 到
到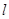 的距离是
的距离是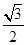 .
.
(Ⅰ)求双曲线的方程;
(Ⅱ)过点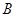 作直线
作直线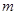 交双曲线于
交双曲线于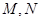 两点,若
两点,若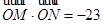 ,求直线
,求直线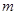 的方程.
的方程.
(本小题满分13分) 已知抛物线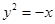 与直线
与直线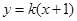 相交于
相交于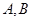 两点.
两点.
(1)求证:以 为直径的圆过坐标系的原点
为直径的圆过坐标系的原点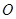 ;(2)当
;(2)当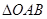 的面积等于
的面积等于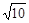 时,求
时,求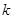 的值.
的值.
(本小题满分12分)已知抛物线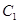 :
: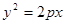 的准线经过双曲线
的准线经过双曲线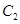 :
: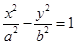 的左焦点,若抛物线
的左焦点,若抛物线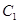 与双曲线
与双曲线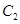 的一个交点是
的一个交点是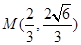 .
.
(1)求抛物线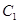 的方程; (2)求双曲线
的方程; (2)求双曲线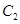 的方程.
的方程.
(本小题满分12分)某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级子棉2吨、二级子棉1吨;生产乙种棉纱需耗一级子棉1吨、二级子棉2吨,每1吨甲种棉纱的利润是600元,每1吨乙种棉纱的利润是900元,工厂在生产这两种棉纱的计划中要求消耗一级子棉不超过300吨、二级子棉不超过250吨.甲、乙两种棉纱应各生产多少,能使利润总额最大?
(本小题满分12分)圆经过点 和
和 .
.
(1)若圆的面积最小,求圆的方程;
(2)若圆心在直线 上,求圆的方程。
上,求圆的方程。