(本小题满分14分)(文科)已知曲线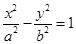
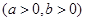 的离心率
的离心率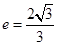 ,直线
,直线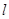 过
过 、
、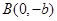 两点,原点
两点,原点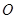 到
到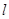 的距离是
的距离是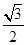 .
.
(Ⅰ)求双曲线的方程;
(Ⅱ)过点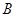 作直线
作直线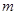 交双曲线于
交双曲线于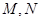 两点,若
两点,若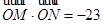 ,求直线
,求直线 的方程.
的方程.
(本小题满分10分)选修4-5:不等式选讲
设函数f(x)=|x-1|+|x-2|.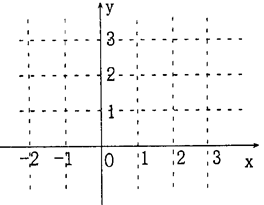
(Ⅰ)画 出函数y=f(x)的图象;
出函数y=f(x)的图象;
(Ⅱ)若不等式|a+b|-|a-b|≤|a|·f(x)对任意a,b∈R且a≠0恒成立,求实数x的范围
(本小题满分10分)选修4-l:几何证明选讲
如图所示,圆O的两弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F,FG切圆O于点G.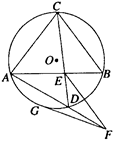
(Ⅰ)求证:△DFE∽△EFA;
(Ⅱ)如果FG=1,求EF的长.
(本小题满分12分)
已知函数f1(x)=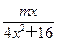 ,f2(x)=
,f2(x)=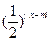 (其中m ∈R且m≠0).
(其中m ∈R且m≠0).
(Ⅰ)讨论函数f1(x)的单调性;
(Ⅱ)若m<-2,求函数f(x)=f1(x)+f2(x)(x∈[-2,2])的最值;
(Ⅲ)设函数g(x)=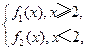 当m≥2时,若对于任意的x1∈[2,+∞),总存在唯一的x2∈(-∞,2),使得g(x1)=g(x2)成立.试求m的取值范围.
当m≥2时,若对于任意的x1∈[2,+∞),总存在唯一的x2∈(-∞,2),使得g(x1)=g(x2)成立.试求m的取值范围.
(本小题满分12分)
已知椭圆C1和抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点,从它们每条曲线 上至少取两个点,将其坐标记录于下表中:
上至少取两个点,将其坐标记录于下表中:
| x |
5 |
-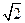 |
4 |
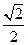 |
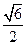 |
| y |
2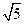 |
0 |
-4 |
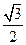 |
-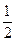 |

(Ⅰ)求C1和C2的方程;
(Ⅱ)过点S(0,-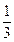 )且斜率为k的动直线l交椭圆C1于A、B两点,在y轴上是否存在定点D,使以线段AB为直径的圆恒过这个点?若存在,求出D的坐标,若不存在,说明理由.
)且斜率为k的动直线l交椭圆C1于A、B两点,在y轴上是否存在定点D,使以线段AB为直径的圆恒过这个点?若存在,求出D的坐标,若不存在,说明理由.
(本小题满分12分)
如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是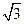 ,D是AC的中点.
,D是AC的中点.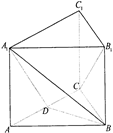
(Ⅰ)求证:B1C∥平面A1BD;
(Ⅱ)求二面角A1-BD-A的大小;
(Ⅲ)求直线AB1与平面A1BD所成的角的正弦值.