(本小题满分10分)选修4-5:不等式选讲
设函数f(x)=|x-1|+|x-2|.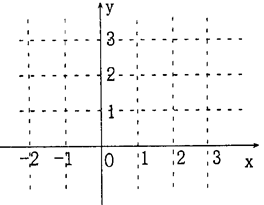
(Ⅰ)画 出函数y=f(x)的图象;
出函数y=f(x)的图象;
(Ⅱ)若不等式|a+b|-|a-b|≤|a|·f(x)对任意a,b∈R且a≠0恒成立,求实数x的范围
已知向量 ,
, .
.
(1)若 ,
, ,且
,且 ,求
,求 ;
;
(2)若 ,求
,求 的取值范围.
的取值范围.
设函数 (其中
(其中 ),
), ,已知它们在
,已知它们在 处有相同的切线.
处有相同的切线.
(1)求函数 ,
, 的解析式;
的解析式;
(2)求函数 在
在 上的最小值;
上的最小值;
(3)若对 恒成立,求实数
恒成立,求实数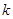 的取值范围.
的取值范围.
过椭圆 的左顶点
的左顶点 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为 ,与
,与 轴的交点为
轴的交点为 ,已知
,已知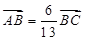 .
.
(1)求椭圆的离心率;
(2)设动直线 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点 ,且与直线
,且与直线 相交于点
相交于点 ,若
,若 轴上存在一定点
轴上存在一定点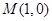 ,使得
,使得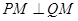 ,求椭圆的方程.
,求椭圆的方程.
已知正项数列 ,其前
,其前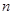 项和
项和 满足
满足 且
且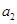 是
是 和
和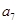 的等比中项.
的等比中项.
(1)求数列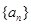 的通项公式;
的通项公式;
(2) 符号 表示不超过实数
表示不超过实数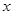 的最大整数,记
的最大整数,记 ,求
,求 .
.
如图,矩形 所在的平面和平面
所在的平面和平面 互相垂直,等腰梯形
互相垂直,等腰梯形 中,
中,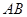 ∥
∥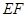 ,
, =2,
=2,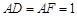 ,
,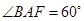 ,
, ,
, 分别为
分别为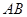 ,
,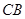 的中点,
的中点, 为底面
为底面 的重心.
的重心.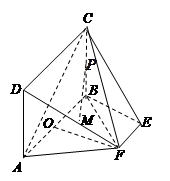
(1)求证: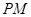 ∥平面
∥平面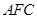 ;
;
(2)求直线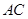 与平面
与平面 所成角的正弦值.
所成角的正弦值.