如图,矩形 所在的平面和平面
所在的平面和平面 互相垂直,等腰梯形
互相垂直,等腰梯形 中,
中,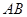 ∥
∥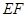 ,
, =2,
=2,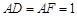 ,
,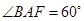 ,
,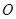 ,
, 分别为
分别为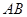 ,
,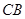 的中点,
的中点, 为底面
为底面 的重心.
的重心.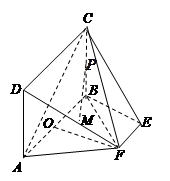
(1)求证: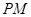 ∥平面
∥平面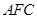 ;
;
(2)求直线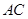 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分15分)已知函数,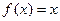 ,
,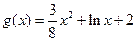 .
.
(Ⅰ)求函数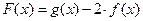 的极大值点与极小值点; (Ⅱ)若函数
的极大值点与极小值点; (Ⅱ)若函数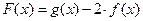 在
在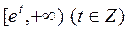 上有零点,求
上有零点,求 的最大值(
的最大值(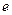 为自然对数的底数); (Ⅲ)设
为自然对数的底数); (Ⅲ)设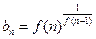 (
(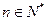 ),试问数列
),试问数列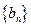 中是否存在相等的两项?若存在,求出所有相等的两项;若不存在,请说明理由.
中是否存在相等的两项?若存在,求出所有相等的两项;若不存在,请说明理由.
(本小题满分14分)在平面直角坐标系中,O为坐标原点,已知向量 又点
又点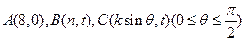 . (Ⅰ)若
. (Ⅰ)若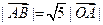 且
且 , 求向量
, 求向量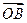 ; (Ⅱ)若向量
; (Ⅱ)若向量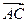 与向量
与向量 共线,当k
共线,当k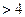 ,且
,且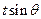 取最大值4时,求
取最大值4时,求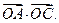
(本小题满分15分)已知数列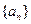 中,
中,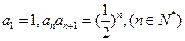 .
.
(Ⅰ)求证:数列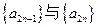 (
(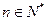 )均为等比数列; (Ⅱ)求数列
)均为等比数列; (Ⅱ)求数列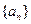 的前
的前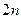 项和
项和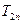 ; (Ⅲ)若数列
; (Ⅲ)若数列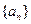 的前
的前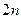 项和为
项和为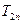 ,不等式
,不等式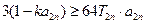 对
对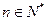 恒成立,求
恒成立,求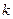 的最大值.
的最大值.
 (本小题满分14分)如下图,某小区准备绿化一块直径为
(本小题满分14分)如下图,某小区准备绿化一块直径为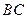 的半圆形空地,
的半圆形空地,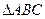 的内接正方形
的内接正方形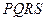 为一水池,
为一水池,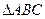 外的地方种草,其余地方种花.若
外的地方种草,其余地方种花.若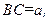
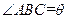 ,设
,设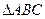 的面积为
的面积为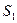 ,正方形
,正方形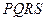 的面积为
的面积为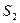 ,将比值
,将比值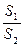 称为“规划合理度”. (Ⅰ)试用
称为“规划合理度”. (Ⅰ)试用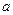 ,
,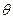 表示
表示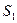 和
和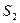 ; (Ⅱ)若
; (Ⅱ)若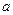 为定值,当
为定值,当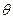 为何值时,“规划合理度”最小?并求出这个最小值.
为何值时,“规划合理度”最小?并求出这个最小值.
(本小题满分14分)设甲、乙两套试验方案在一次试验中成功的概率均为p,且这两套试验方案中至少有一套试验成功的概率为0.51,假设这两套试验方案在试验过程中,相互之间没有影响.,设试验成功的方案的个数为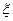 .(Ⅰ)求p的值;(Ⅱ)求
.(Ⅰ)求p的值;(Ⅱ)求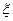 的数学期望E
的数学期望E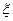 与方差D
与方差D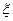 .
.