为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.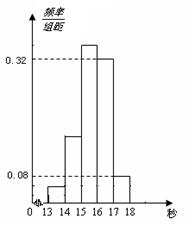
已知椭圆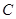 :
: 的离心率为
的离心率为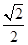 ,左焦点为
,左焦点为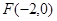 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若直线 与曲线
与曲线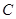 交于不同的
交于不同的 、
、 两点,且线段
两点,且线段 的中点
的中点 在圆
在圆 上,求
上,求 的值.
的值.
某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110), [140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题.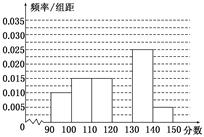
(Ⅰ)求分数在[120,130)内的频率;
(Ⅱ)若在同一组数据中,将该组区间的中点值(如:组区间[100,110)的中点值为=105)作为这组数据的平均分,据此估计本次考试的平均分;
(Ⅲ)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
数列 的前
的前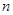 项和为
项和为 ,
, .
.
(Ⅰ)设 ,证明:数列
,证明:数列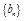 是等比数列;
是等比数列;
(Ⅱ)求数列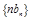 的前
的前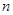 项和
项和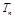 .
.
如图,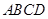 是边长为2的正方形,
是边长为2的正方形,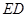 ⊥平面
⊥平面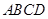 ,
, ,
,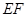 //
//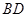 且
且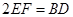 .
.
(Ⅰ)求证:平面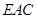 ⊥平面
⊥平面 ;
;
(Ⅱ)求几何体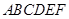 的体积.
的体积.
已知函数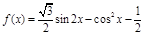 ,
,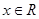 .
.
(Ⅰ)求函数 的最小值和最小正周期;
的最小值和最小正周期;
(Ⅱ)设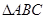 的内角
的内角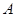 、
、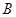 、
、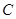 的对边分别为
的对边分别为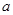 、
、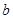 、
、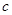 ,满足
,满足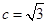 ,
,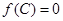 且
且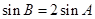 ,求
,求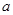 、
、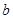 的值.
的值.