某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110), [140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题.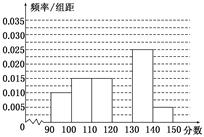
(Ⅰ)求分数在[120,130)内的频率;
(Ⅱ)若在同一组数据中,将该组区间的中点值(如:组区间[100,110)的中点值为=105)作为这组数据的平均分,据此估计本次考试的平均分;
(Ⅲ)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
在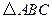 中,
中,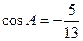 ,
,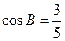 .
.
(1)求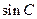 的值;
的值;
(2)设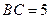 ,求
,求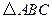 的面积.
的面积.
( 本题满分10分)
本题满分10分)
如图,已知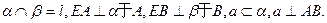 求证:a∥l.
求证:a∥l.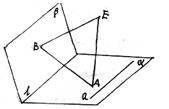
已知函数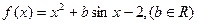 ,且对任意
,且对任意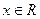 ,有
,有 .
.
(1)求 ;
;
(2)已知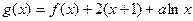 在区间(0,1)上为单调函数,求实
在区间(0,1)上为单调函数,求实 数
数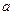 的取值范围.
的取值范围.
(3)讨论函数 的零点个数?(提示
的零点个数?(提示 :
: )
)

如图,抛物线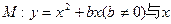 轴交于O,A两点,交直线
轴交于O,A两点,交直线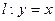 于O,B两点,经过三
于O,B两点,经过三 点O,A,B作圆C
点O,A,B作圆C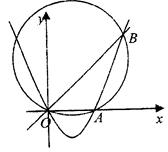
(I)求证:当b变化时,圆C的圆心在一条定直线上;
(II)求证: 圆C经过除原点外的一个定点;
圆C经过除原点外的一个定点;
(III)是否存在这样的抛物线M,使它的顶点与C的距离不大于圆C的半径?
已知圆A: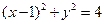 与x轴负半轴交于B点,过B的弦BE与y轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆.
与x轴负半轴交于B点,过B的弦BE与y轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆.
(1)求椭圆的方程;
(2)点P在椭圆C上运动,点Q在圆A上运动,求PQ+PD的最大值.