以下茎叶图记录了甲,乙两组各四名同学的植树棵树,乙组记录中有一个数据模糊,无法确认,在图中以X表示。
(1)如果X=8,求乙组同学植树棵树的平均数和方差;
(2)如果X=9,分别从甲,乙两组中随机选取一名同学,求这两名同学的植树总棵树为19的概率.
已知命题p:方程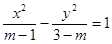 表示焦点在
表示焦点在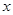 轴上的双曲线,命题q:f(x)=-(5-2m)x是减函数,若p或q为真命题,p且q为假命题,求实数m的取值范围
轴上的双曲线,命题q:f(x)=-(5-2m)x是减函数,若p或q为真命题,p且q为假命题,求实数m的取值范围
设O为坐标原点,点P的坐标(x-2,x-y).
(1)在一个盒子中,放有标号为1,2,3的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为x,y,求|OP|的最大值,并求事件“|OP|取到最大值”的概率;
(2)若利用计算机随机在[0,3]上先后取两个数分别记为x,y,求P点在第一象限的概率.
在平面直角坐标系中,已知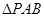 的两个顶点坐标分别是
的两个顶点坐标分别是 、
、 ,另两边
,另两边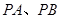 的斜率之积为
的斜率之积为 .
.
(1)求顶点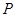 的轨迹
的轨迹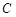 的方程;
的方程;
(2)若轨迹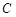 上点
上点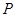 与轨迹
与轨迹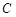 的两焦点构成
的两焦点构成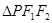 ,且
,且 =
= , 求
, 求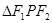 的面积
的面积
设命题p :方程 有两个不等的负实根; 命题q :方程
有两个不等的负实根; 命题q :方程
 无实根. 若命题p或q为真命题,命题p且q为假命题,求实数m的取值范围.
无实根. 若命题p或q为真命题,命题p且q为假命题,求实数m的取值范围.