工厂用两种原料A、B配成甲、乙两种药品,每生产一箱甲药品使用4kg的A原料,耗时1小时,每生产一箱乙药品使用4kg的B原料,耗时2小时,该厂每天最多可从原料厂获取16kg的A原料和12kg的B原料,每天只能有8小时的合成生产时间,该厂生产一箱甲药品获得3万元,生产一箱乙药品获得1万元,怎样安排生产才能获利最大?最大利润是多少?
已知等差数列数列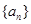 的前
的前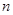 项和为
项和为 ,等比数列
,等比数列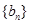 的各项均为正数,公比是
的各项均为正数,公比是 ,且满足:
,且满足: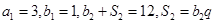 .
.
(Ⅰ)求 与
与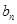 ;
;
(Ⅱ)设 ,若
,若 满足:
满足: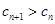 对任意的
对任意的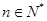 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 中,三个内角A、B、C所对的边分别为
中,三个内角A、B、C所对的边分别为 、
、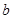 、
、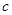 ,若
,若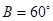 ,
,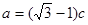 .
.
(Ⅰ)求角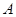 的大小;
的大小;
(Ⅱ)已知 的面积为
的面积为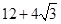 ,求函数
,求函数 的最大值.
的最大值.
已知函数 ,设方程
,设方程 有两个实数根
有两个实数根
(1)若果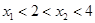 ,设函数
,设函数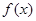 的对称轴为
的对称轴为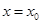 ,求证:
,求证: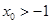
(2)如果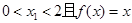 的两个实数根相差2,求实数b的取值范围。
的两个实数根相差2,求实数b的取值范围。
(本题满分为15分)如图,焦点在 轴的椭圆,离心率
轴的椭圆,离心率 ,且过点
,且过点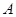 (-2,1),由椭圆上异于点
(-2,1),由椭圆上异于点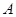 的
的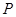 点发出的光线射到
点发出的光线射到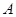 点处被直线
点处被直线 反射后交椭圆于
反射后交椭圆于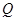 点(
点(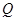 点与
点与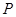 点不重合).
点不重合).
(1)求椭圆标准方程;
(2)求证:直线 的斜率为定值;
的斜率为定值;
(3)求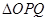 的面积的最大值.
的面积的最大值.
(本题满分为15分)如图,已知长方形 中,
中,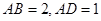 ,
, 为
为 的中点.将
的中点.将 沿
沿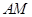 折起,使得平面
折起,使得平面 平面
平面 .
.
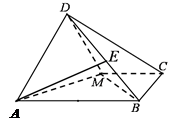
(1)求证: ;
;
(2)若点 是线段
是线段 上的一动点,问点E在何位置时,二面角
上的一动点,问点E在何位置时,二面角 的余弦值为
的余弦值为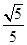 .
.