（本小题12分）已知直线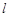
的参数方程是
，圆C的极坐标方程为
．
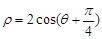（1）求圆心C的直角坐标；
（2）由直线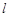上的点向圆C引切线，求切线长的最小值．
（本小题10分）已知
：方程
有两个不相等的负实根；
：方程
无实根，如果或为真，且为假，求
的取值范围。
（本小题满分12分）已知函数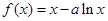
，
．
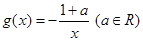（Ⅰ）若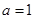
，求函数
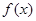的极值；
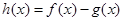（Ⅱ）设函数
，求函数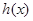
的单调区间；
（Ⅲ）若在区间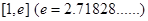
上不存在
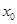，使得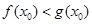
成立，求实数
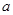的取值范围．
在平面直角坐标系xOy中，已知两点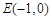
和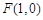
，动点M满足
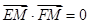，设点M的轨迹为C，半抛物线
：
（
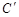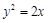），设点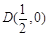
．
（Ⅰ）求C的轨迹方程；
（Ⅱ）设点T是曲线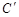上一点，曲线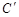在点T处的切线与曲线C相交于点A和点B，求△ABD的面积的最大值及点T的坐标．
一块长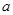为
、宽为
的长方形铁片，铁片的四角截去四个边长均为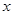
的小正方形，然后做成一个无盖方盒．
（Ⅰ）试把方盒的容积V表示为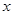的函数；
（Ⅱ）试求方盒容积V的最大值．
满足
，且对任意
都有
的值并证明函数
对任意
恒成立，求实数m的取值范围。