.
已知等差数列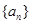 的首项为
的首项为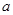 ,公差为b,等比数列
,公差为b,等比数列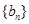 的首项为b,公比为a(其中a,b均为正整数)。
的首项为b,公比为a(其中a,b均为正整数)。
(I)若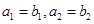 ,求数列
,求数列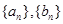 的通项公式;
的通项公式;
(II)对于(1)中的数列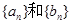 ,对任意
,对任意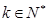 在
在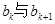 之间插入
之间插入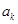 个2,得到一个新的数列
个2,得到一个新的数列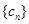 ,试求满足等式
,试求满足等式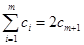 的所有正整数m的值;
的所有正整数m的值;
(III)已知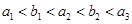 ,若存在正整数m,n以及至少三个不同的b值使得等
,若存在正整数m,n以及至少三个不同的b值使得等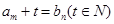 成立,求t的最小值,并求t最小时a,b的值。
成立,求t的最小值,并求t最小时a,b的值。
(本小题满分13分)如图,在三棱柱ABC—A1B1C1中,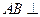 侧面BB1C1C,已知AB=BC=1,BB1=2,
侧面BB1C1C,已知AB=BC=1,BB1=2,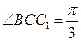 ,E为CC1的中点。
,E为CC1的中点。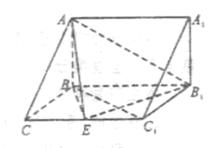
(1)求证: 平面ABC;
平面ABC;
(2)求二面角A—B1E—B的大小。
(本小题满分12分)
已知等比数列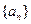 的公比是q,且
的公比是q,且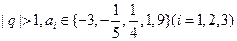
(1)求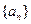 的通项公式;
的通项公式;
(2)若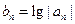 ,求数列
,求数列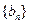 的前n项和
的前n项和
(本小题满分12分)
已知向量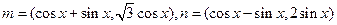 ,若函数
,若函数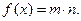
(1)求函数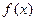 的单调递增区间;
的单调递增区间;
(2)在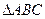 中,a,b,c分别是内角A,B,C的对边,且
中,a,b,c分别是内角A,B,C的对边,且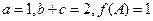 ,求角A、B、C的大小。
,求角A、B、C的大小。
(本题满分14分) 设函数f (x)=ln x+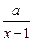 在(0,
在(0,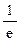 ) 内有极值.
) 内有极值.
(Ⅰ) 求实数a的取值范围;
(Ⅱ) 若x1∈(0,1),x2∈(1,+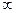 ).求证:f (x2)-f (x1)>e+2-
).求证:f (x2)-f (x1)>e+2-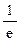 .
.
注:e是自然对数的底数.
(本题满分15分) 如图,椭圆C: x2+3y2=3b2(b>0).
(Ⅰ) 求椭圆C的离心率;
(Ⅱ) 若b=1,A,B是椭圆C上两点,且| AB | =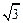 ,求△AOB面积的最大值.
,求△AOB面积的最大值.