(本小题满分12分)
定义在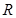 上的函数
上的函数 同时满足以下条件:
同时满足以下条件:
① 在
在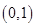 上是减函数,在
上是减函数,在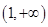 上是增函数;②
上是增函数;②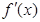 是偶函数;
是偶函数;
③ 在
在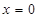 处的切线与直线
处的切线与直线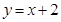 垂直.
垂直.
(1)求函数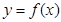 的解析式;
的解析式;
(2)设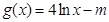 ,若存在
,若存在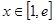 ,使
,使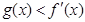 ,求实数
,求实数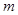 的取值范围.
的取值范围.
已知函数f(x)= x3-ax+1.
x3-ax+1.
(1)求x=1时,f(x)取得极值,求a的值;
(2)求f(x)在[0,1]上的最小值;
(3)若对任意m∈R,直线y=-x+m都不是曲线y=f(x)的切线,求a的取值范围.
某幼儿园准备建一个转盘,转盘的外围是一个周长为k米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连经预算,转盘上的每个座位与支点相连的钢管的费用为3k元/根,且当两相邻的座位之间的圆弧长为x米时,相邻两座位之间的钢管和其中一个座位的总费用为 k元.假设座位等距分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记转盘的总造价为y元.
k元.假设座位等距分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记转盘的总造价为y元.
(1)试写出y关于x的函数关系式,并写出定义域;
(2)当k=50米时,试确定座位的个数,使得总造价最低?
已知函数f(x)= ax3+(a-2)x+c的图象如图所示.
ax3+(a-2)x+c的图象如图所示.
(1)求函数y=f(x)的解析式;
(2)若g(x)= -2ln x在其定义域内为增函数,求实数k的取值范围.
-2ln x在其定义域内为增函数,求实数k的取值范围.
设L为曲线C:y= 在点(1,0)处的切线.
在点(1,0)处的切线.
(1)求L的方程;
(2)证明:除切点(1,0)之外,曲线C在直线L的下方.
已知函数f(x)=2x+k·2-x,k∈R.
(1)若函数f(x)为奇函数,求实数k的值;
(2)若对任意的x∈[0,+∞)都有f(x)>2-x成立,求实数k的取值范围.