(本小题满分14分)
给定椭圆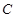 :
: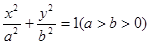 . 称圆心在原点
. 称圆心在原点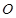 ,半径为
,半径为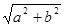 的圆是椭圆
的圆是椭圆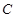 的“准圆”. 若椭圆
的“准圆”. 若椭圆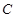 的一个焦点为
的一个焦点为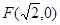 ,其短轴上的一个端点到
,其短轴上的一个端点到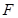 的距离为
的距离为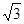 .
.
(1)求椭圆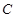 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点 是椭圆
是椭圆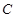 的“准圆”上的一个动点,过动点
的“准圆”上的一个动点,过动点 作直线
作直线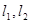 ,使得
,使得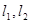 与椭圆
与椭圆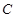 都只有一个交点,试判断
都只有一个交点,试判断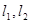 是否垂直?并说明理由.
是否垂直?并说明理由.
某工厂2008年的生产总值100万元,技术革新后预计以后每年的生产总值比上一年增加5%,问最早需要哪一年年生产总值超过200万元.写出计算的一个算法。
是否存在常数a、b、c,使等式 对一切正整数n都成立?证明你的结论
对一切正整数n都成立?证明你的结论
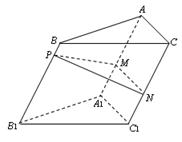
如图,点 为斜三棱柱
为斜三棱柱 的侧棱
的侧棱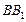 上一点,
上一点,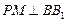 交
交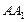 于点
于点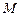 ,
,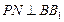 交
交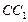 于点
于点 .
.
(1) 求证: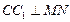 ;
;
(2) 在任意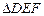 中有余弦定理:
中有余弦定理: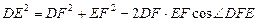 . 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
( 14分)已知函数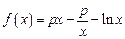 ,
,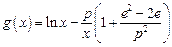 ,其中
,其中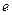 为无理数
为无理数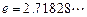 .(1)若
.(1)若 ,求证:
,求证: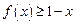 ;(2)若
;(2)若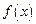 在其定义域内是单调函数,求
在其定义域内是单调函数,求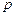 的取值范围;(3)对于区间(1,2)中的任意常数
的取值范围;(3)对于区间(1,2)中的任意常数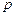 ,是否存在
,是否存在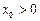 使
使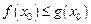 成立?
成立?
若存在,求出符合条件的一个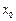 ;否则,说明理由.
;否则,说明理由.
已知 (I)若a=3,求
(I)若a=3,求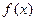 的单调区间和极值;(II)已知
的单调区间和极值;(II)已知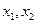 是
是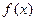 的两个不同的极值点,且
的两个不同的极值点,且 ,若
,若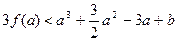 恒成立,求实数
恒成立,求实数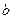 的取值范围.
的取值范围.