如图所示,在水平匀速运动的传送带的左端(P点),无初速地轻放一质量为m=1kg的物块,物块随传送带运动到A点后抛出,物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑。B、D为圆弧的两端点,其连线水平。已知圆弧半径R=1.0m,圆弧对应的圆心角θ=106º,轨道最低点为C,A点距水平面的高度h=0.80m。(g取10m/s2,sin53º=0.8,cos53º=0.6)求⑴物块离开A点时水平初速度的大小⑵物块经过C点时对轨道压力的大小⑶若PA间的距离为1.5m, 传送带的速度为5m/s,求物块与传送带间的动摩擦因数

如图所示的电路中,R1=1Ω,R2=6Ω,电源内阻r=1Ω,若开关闭合后通过电源的电流为3A,铭牌上标有“6V 12W”的电动机刚好正常工作,求:
(1)流过R2上的电流为多少?
(2)电源电动势为多少?
(3)若电动机线圈电阻为,电动机输出功率为多少?
如图所示,真空中有以O1为圆心,r为半径的圆形匀强磁场区域,坐标原点O为圆形磁场边界上的一点。磁场的磁感应强度大小为B,方向垂直于纸面向外。x=r的虚线右侧足够大的范围内有方向竖直向下、大小为E的匀强电场。从O点在纸面内向各个不同方向发射速率相同的质子,设质子在磁场中的偏转半径也为r,已知质子的电荷量为e,质量为m。求: 
(1)质子射入磁场时的速度大小;
(2)速度方向沿y轴正方向射入磁场的质子到达x轴所需的时间;
(3)速度方向与y轴正方向成37°角且与x轴正方向成127°角射入磁场的质子到达x轴时的位置坐标。(已知sin37°=0.6,cos37°="0.8)"
(15分)如图所示,两根完全相同的“V”字形导轨OPQ与KMN倒放在绝缘水平面上,两导轨都在竖直平面内且正对、平行放置,其间距为L,电阻不计。两条导轨足够长,所形成的两个斜面与水平面的夹角都是α.两个金属棒ab和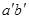 的质量都是m,电阻都是R,与导轨垂直放置且接触良好.空间有竖直向下的匀强磁场,磁感应强度为B.
的质量都是m,电阻都是R,与导轨垂直放置且接触良好.空间有竖直向下的匀强磁场,磁感应强度为B. 
(1)如果两条导轨皆光滑,让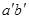 固定不动,将ab释放,则ab达到的最大速度是多少?
固定不动,将ab释放,则ab达到的最大速度是多少?
(2)如果将ab与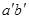 同时释放,它们所能达到的最大速度分别是多少?
同时释放,它们所能达到的最大速度分别是多少?
(15分) 薄木板长L=1m,质量M=9kg在动摩擦因数μ1=0.1的水平地面上向右滑行,当木板速度v0=2m/s时,在木板的右端轻放一质量m=1kg的小铁块(可视为质点)如图所示,当小铁块刚好滑到木板左端时,铁块和木板达到共同速度。取g=10m/s2,求:
(1)从铁块放到木板上到它们达到相同速度所用的时间t;
(2)小铁块与木板间的动摩擦因数μ2 。
如图所示,质量M="4" kg的小车放在水平光滑的平面上,在小车左端加一水平推力F=6N,当小车向右运动的速度达到2 m/s时,在小车前端轻轻地放上一个大小不计,质量为m="1" kg的小物块,物块与小车间的动摩擦因数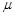 =0.2,小车足够长。g取10m/s2,求:
=0.2,小车足够长。g取10m/s2,求: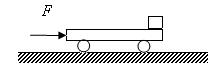
(1)小物块放后,小物块及小车的加速度各为多大;
(2)经多长时间两者达到相同的速度;
(3)从小物块放上小车开始,经过t=4s小物块通过的位移大小为多少。