1879年美国物理学家霍尔在研究载流导体在磁场中受力情况时,发现了一种新的电磁效应:将导体置于磁场中,并沿垂直磁场方向通入电流,则在导体中垂直于电流和磁场的方向会产生一个横向电势差,这种现象后来被称为霍尔效应,这个横向的电势差称为霍尔电势差。
(1)如图14甲所示,某长方体导体 的高度为
的高度为 、宽度为
、宽度为 ,其中的载流子为自由电子,其电荷量为
,其中的载流子为自由电子,其电荷量为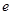 ,处在与
,处在与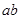
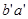 面垂直的匀强磁场中,磁感应强度为
面垂直的匀强磁场中,磁感应强度为 。在导体中通有垂直于
。在导体中通有垂直于 面的电流,若测得通过导体的恒定电流为
面的电流,若测得通过导体的恒定电流为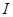 ,横向霍尔电势差为
,横向霍尔电势差为 ,求此导体中单位体积内自由电子的个数。
,求此导体中单位体积内自由电子的个数。
(2)对于某种确定的导体材料,其单位体积内的载流子数目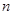 和载流子所带电荷量
和载流子所带电荷量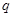 均为定值,人们将
均为定值,人们将 定义为该导体材料的霍尔系数。利用霍尔系数
定义为该导体材料的霍尔系数。利用霍尔系数 已知的材料可以制成测量磁感应强度的探头,有些探头的体积很小,其正对横截面(相当于图14甲中的
已知的材料可以制成测量磁感应强度的探头,有些探头的体积很小,其正对横截面(相当于图14甲中的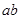
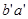 面)的面积可以在
面)的面积可以在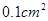 以下,因此可以用来较精确的测量空间某一位置的磁感应强度。如图14乙所示为一种利用霍尔效应测磁感应强度的仪器,其中的探头装在探杆的前端,且使探头的正对横截面与探杆垂直。这种仪器既可以控制通过探头的恒定电流的大小
以下,因此可以用来较精确的测量空间某一位置的磁感应强度。如图14乙所示为一种利用霍尔效应测磁感应强度的仪器,其中的探头装在探杆的前端,且使探头的正对横截面与探杆垂直。这种仪器既可以控制通过探头的恒定电流的大小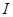 ,又可以监测出探头所产生的霍尔电势差
,又可以监测出探头所产生的霍尔电势差 ,并自动计算出探头所测位置磁场的磁感应强度的大小,且显示在仪器的显示窗内。
,并自动计算出探头所测位置磁场的磁感应强度的大小,且显示在仪器的显示窗内。
①在利用上述仪器测量磁感应强度的过程中,对探杆的放置方位有何要求;
②要计算出所测位置磁场的磁感应强度,除了要知道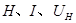 外,还需要知道哪个物理量,并用字母表示。推导出用上述这些物理量表示所测位置磁感应强度大小的表达式。
外,还需要知道哪个物理量,并用字母表示。推导出用上述这些物理量表示所测位置磁感应强度大小的表达式。
一个质量为m的重球自高h1处由静止下落,落到雪上后陷入雪中的深度为h2.已知空气和雪对球的阻力恒定,空气的阻力为f1,求雪对球的阻力f2.
一个质量为60 kg的物体,和水平地面间的动摩擦因数为0.2.一个人用和地面成30°角的力F1拉它,另一个人用和地面成30°角的力F2推它,如图6-2-14所示,已知F1="400" N,F2="200" N,g取10 m/s2.求物体运动的加速度.
图6-2-14
如图所示,一根重8N的均匀直棒AB,A端用细绳吊在固定点O上,现用一水平方向6N的力作用于棒的B端。试求绳跟竖直方向成多大角度时才平衡?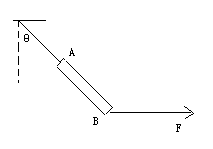
一人通过箱带拉着一个旅行箱前进,拉力是12 N,箱带与水平面夹角是30°,则拉力的水平分力是多大?竖直分力是多大?
如图7所示,物块和斜面体的质量分别为m.M,物块在平行于斜面的推力F作用下沿斜面加速度a向上滑动时,斜面体仍保持静止.斜面倾角为θ,试求地面对斜面体的支持力和摩擦力.