已知函数 的一系列对应值如下表:
的一系列对应值如下表:
 |
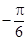 |
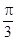 |
 |
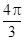 |
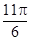 |
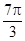 |
 |
 |
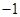 |
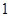 |
 |
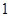 |
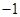 |
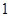 |
 |
(1)根据表格提供的数据求函数 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数 周期为
周期为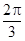 ,当
,当 时,方程
时,方程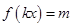 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围.
的取值范围.
已知函数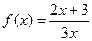 ,数列
,数列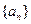 满足
满足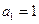 ,
,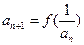 ,
,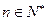 .
.
(1)求数列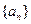 的通项公式;
的通项公式;
(2)令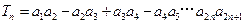 ,求
,求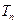 ;
;
(3)令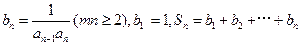 ,若
,若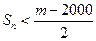 对一切
对一切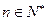 成立,求最小正整数
成立,求最小正整数 .
.
已知函数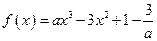
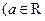 且
且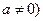 ,求函数
,求函数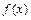 的极大值与极小值.
的极大值与极小值.
已知:双曲线的顶点坐标(0,1),(0,-l),离心率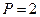 ,又抛物线
,又抛物线 的焦点与双曲线一个焦点重合.
的焦点与双曲线一个焦点重合.
(1)求抛物线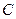 的方程;
的方程;
(2)已知 是
是 轴上的两点,过
轴上的两点,过 做直线与抛物线
做直线与抛物线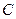 交于
交于 两点,试证:直线
两点,试证:直线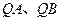 与
与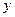 轴所成的锐角相等.
轴所成的锐角相等.
(3)在(2)的前提下,若直线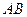 的斜率为1,问
的斜率为1,问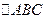 的面积是否有最大值?若有,求出最大值.若没有,说明理由.
的面积是否有最大值?若有,求出最大值.若没有,说明理由.
已知函数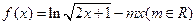 .
.
(1)求函数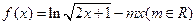 的单调区间;
的单调区间;
(2)若函数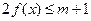 恒成立,求
恒成立,求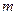 的取值范围.
的取值范围.
已知四棱锥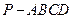 中,
中,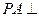 平面
平面 ,底面
,底面 为菱形,
为菱形,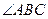 =60
=60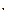 ,
, ,
,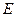 是线段
是线段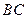 的中点.
的中点.
(1)求证: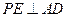 ;
;
(2)求平面 与平面
与平面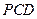 所成锐二面角的大小;
所成锐二面角的大小;
(3)在线段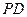 上是否存在一点
上是否存在一点 ,使得
,使得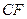 ∥平面PAE,并给出证明.
∥平面PAE,并给出证明.