.小明在学习了“除零以外的任何数的零次幂的值为1”后遇到这样一道题:如果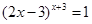 ,求x的值,他解出来的结果为
,求x的值,他解出来的结果为 ,老师说小明考虑问题不全面,你能帮助小明解决这个问题吗?
,老师说小明考虑问题不全面,你能帮助小明解决这个问题吗?
已知关于x的一元二次方程mx2﹣(m+2)x+2=0.
(1)证明:不论m为何值时,方程总有实数根;
(2)m为何整数时,方程有两个不相等的正整数根.
如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.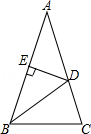
(1)写出图中一对全等三角形和一对相似比不为1的相似三角形;
(2)选择(1)中一对加以证明.
(本题14分)如图,在平面直角坐标系中,直线AB与x轴交于点A(4,0),与y轴交于点B(0,4),抛物线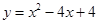 的的顶点为E.点C的坐标为(0,m)(m≠4),点C关于AB的对称点是点D,连结BD,CD,CE,DE
的的顶点为E.点C的坐标为(0,m)(m≠4),点C关于AB的对称点是点D,连结BD,CD,CE,DE
(1)当点C在线段OB上时,求证:△BCD是等腰直角三角形;
(2)当m>0时,若△CDE为直角三角形,求tan∠CEO的值;
(3)设点P是该抛物线上一点,是否存在m的值,使以P,C,D,E为顶点的四边形为平行四边形,若存在,请直接写出所有满足条件的m的值;若不存在,请说明理由.
(本题12分)温州儿童玩具畅销国内外,工人小李在童星玩具厂工作.已知该厂生产A,B两种产品,小李生产1件A产品和1件B产品需35分钟;生产3件A产品和2件B产品需85分钟.
(1)小李生产1件A产品和B产品各需要几分钟?
(2)已知该厂工资待遇为:按件计酬,多劳多得,每月另加福利工资300元,全勤奖300元,按月结算.工人每生产一件A种产品和B产品分别可得报酬2.0元、2.6元,小李可能被分配到生产A,B两种产品中的一种或两种.
①如果小李可以自己选择一种产品生产,他选择哪种更合算?说明理由.
②如果小李4月份工作22天,每天8小时,且享受了该月的福利工资和全勤奖,试确定小李该月的工资收入范围.
(本题10分)如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE。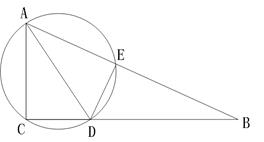
(1)求证:AC=AE;
(2)求△ACD外接圆的半径。