如图,已知直角梯形ACDE所在的平面垂直于平面ABC,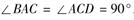 ,
,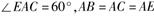
(I )在直线BC上是否存在一点P,使得DP//平面EAB?请证明你的结论;
(II)求平面EBD与平面ABC所成的锐二面角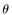 的余弦值.
的余弦值.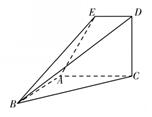
已知数列 的通项公式为
的通项公式为
(1)试求 的值;
的值;
(2)猜想 的值,并用数学归纳法证明你的猜想.
的值,并用数学归纳法证明你的猜想.
一个口袋内有4个不同的红球,6个不同的白球.
(1)从中任取4个球,红球个数不少于白球个数的取法有多少种?
(2)若取一个红球记2分,取一个白球记1分,从中任取5个球,使总分不少于7的取法
已知函数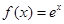 ,其图像在点
,其图像在点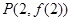 处的切线为
处的切线为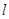 .
.
(1)求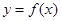 、直线
、直线 及两坐标轴围成的图形绕
及两坐标轴围成的图形绕 轴旋转一周所得几何体的体积;
轴旋转一周所得几何体的体积;
(2)求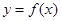 、直线
、直线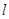 及
及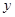 轴围成图形的面积.
轴围成图形的面积.
设存在复数z同时满足下列条件:
(1)复数z在复平面内对应点位于第二象限;
(2)z· +2iz=8+ai (a∈R),试求a的取值范围.
+2iz=8+ai (a∈R),试求a的取值范围.
函数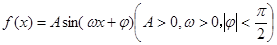 的一段图象如图所示.
的一段图象如图所示.
(1)求函数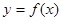 的解析式;
的解析式;
(2)将函数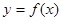 的图象向右平移
的图象向右平移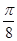 个单位,得到
个单位,得到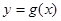 的图象,求直线
的图象,求直线 与函数
与函数 的图象在
的图象在 内所有交点的坐标.
内所有交点的坐标.