.(本小题满分12分)
设函数f(x)=lnx-p(x-1),p∈R.
(Ⅰ)当p=1时,求函数f(x)的单调区间;
(Ⅱ)设函数g(x)=xf(x)+p(2x2―x―1),(x≥1),求证:当p≤-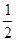 时,有g(x)≤0成立.
时,有g(x)≤0成立.
某企业11年底投入100万元,购入一套污水处理设备,该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费是2万元,由于设备老化,以后每年的维护费用都比上一年增加2万元.
⑴求该企业使用设备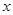 年的年平均污水处理费用(年平均污水处理费用=
年的年平均污水处理费用(年平均污水处理费用= )
)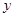 万元;
万元;
⑵为使该企业的年平均污水处理费用最低,问几年后需要重新更换新的污水处理设备?
已知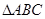 ,内角
,内角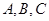 所对的边分别为
所对的边分别为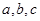 ,且满足下列三个条件:①
,且满足下列三个条件:①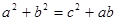 ②
②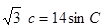 ③
③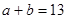
求 (1) 内角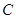 和边长
和边长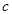 的大小;
的大小;
(2) 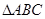 的面积.
的面积.
在等差数列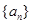 中,
中, ,
,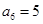 .
.
(1)求数列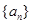 的通项公式;
的通项公式;
(2)如果 ,求数列
,求数列 的前10项的和
的前10项的和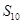 .
.
已知 ,
,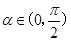 ,
,
(1)求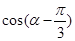 的值;(2)求
的值;(2)求 的值.
的值.
已知函数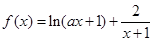 ,其中
,其中 .
.
(1)若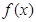 在
在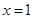 处取得极值,求曲线
处取得极值,求曲线 在点
在点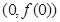 处的切线方程;
处的切线方程;
(2)讨论函数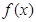 在
在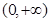 的单调性;
的单调性;
(3)若函数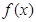 在
在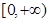 上的最小值为2,求
上的最小值为2,求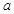 的取值范围.
的取值范围.