. (本小题满分12分)
如图,设抛物线C1: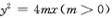 的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率
的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率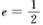 的椭圆C2与抛物线C1在X轴上方的交点为P,延长PF2交抛物线于点Q,M是抛物线上一动点,且M在P与Q之间运动.
的椭圆C2与抛物线C1在X轴上方的交点为P,延长PF2交抛物线于点Q,M是抛物线上一动点,且M在P与Q之间运动.
(I)当m =1时,求椭圆C2的方程;
(II)当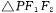 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求 面积的最大值.
面积的最大值.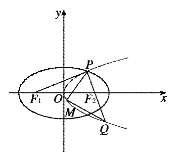
已知函数 .
.
(1)当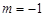 时,求函数
时,求函数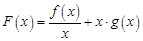 在
在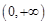 上的极值;
上的极值;
(2)若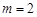 ,求证:当
,求证:当 时,
时,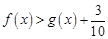 .
.
(参考数据: )
)
已知椭圆 的离心率为
的离心率为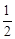 ,左.右焦点分别是
,左.右焦点分别是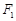 ,
, ,点
,点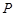 为椭圆
为椭圆 上任意一点,且
上任意一点,且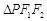 面积最大值为
面积最大值为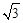 .
.
(1)求椭圆 的方程;
的方程;
(2)过 作垂直于
作垂直于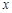 轴的直线
轴的直线 交椭圆于
交椭圆于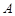 .
. 两点(点
两点(点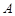 在第一象限),
在第一象限), .
. 是椭圆上位于直线
是椭圆上位于直线 两侧的动点,若
两侧的动点,若 ,求证:直线
,求证:直线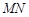 的斜率为定值.
的斜率为定值.
已知抛物线 的焦点为
的焦点为 ,抛物线
,抛物线 的焦点为
的焦点为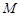 .
.
(1)若过点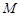 的直线
的直线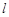 与抛物线
与抛物线 有且只有一个交点,求直线
有且只有一个交点,求直线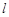 的方程;
的方程;
(2)若直线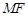 与抛物线
与抛物线 交于
交于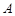 .
. 两点,求
两点,求 的面积.
的面积.
在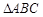 中,已知角
中,已知角 .
.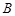 .
.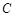 的对边分别为
的对边分别为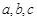 ,且
,且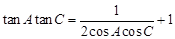 .
.
(1)求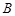 的大小;
的大小;
(2)若 ,试判断
,试判断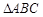 的形状.
的形状.
设等差数列 的前
的前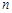 项和为
项和为 ,
, ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)设数列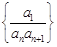 的前
的前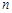 项和为
项和为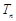 ,求证:
,求证: .
.