已知椭圆 的离心率为
的离心率为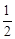 ,左.右焦点分别是
,左.右焦点分别是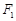 ,
, ,点
,点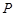 为椭圆
为椭圆 上任意一点,且
上任意一点,且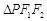 面积最大值为
面积最大值为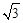 .
.
(1)求椭圆 的方程;
的方程;
(2)过 作垂直于
作垂直于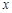 轴的直线
轴的直线 交椭圆于
交椭圆于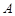 .
. 两点(点
两点(点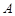 在第一象限),
在第一象限), .
. 是椭圆上位于直线
是椭圆上位于直线 两侧的动点,若
两侧的动点,若 ,求证:直线
,求证:直线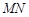 的斜率为定值.
的斜率为定值.
已知函数 的定义域为集合
的定义域为集合 ,
, 的定义域为集合
的定义域为集合 ,集合
,集合
(1)若 ,求实数
,求实数 的取值范围.
的取值范围.
(2)如果若 则
则 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围.
已知向量
(1)若 分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足
分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足 的概率.
的概率.
(2)若 在连续区间[1,6]上取值,求满足
在连续区间[1,6]上取值,求满足 的概率.
的概率.
已知圆 的圆心与点
的圆心与点 关于直线
关于直线 对称,直线
对称,直线 与圆
与圆 相交于
相交于 、
、 两点,且
两点,且 ,求圆
,求圆 的方程.
的方程.
甲、乙两艘货轮都要在某个泊位停靠6小时,假定它们在一昼夜的时间段中随机到达,试求两船中有一艘在停泊位时,另一艘船必须等待的概率.
为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图所示).已知图中从左到右的前3个小组的频率之比为1∶2∶3,第2小组的频数为12,求抽取的学生人数.