2011年国家对“酒后驾车”加大了处罚力度,出台了不准酒后驾车的禁令,某记者在一停车场对开车的司机进行了相关的调查,本次调查结果共有四种情况:①有时会喝点酒开车;②已戒酒或从不喝酒;③酒后不开车或请专业司机代驾;④平时喝酒,但开车当天不喝酒。将这次调查情况整理并绘制成如下尚不完整的统计图,请根据相关信息,解答下列问题。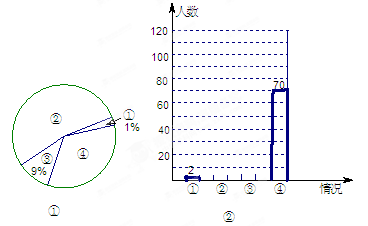
(1)该记者本次一共调查
了 名司机。
(2)求图①中④所在扇形的圆心角,并补全图②。
(3)在本次调查中,记者随机采访其中一名司机,求他属于第②种情况的概率。
(4)请估计在开车的10万名司机中,不违反“酒驾”禁令的人数。
按要求完成下面题目: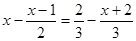
解:去分母,得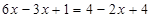 ①
①
即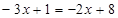 ……②
……②
移项,得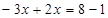 ③
③
合并同类项,得 ④
④
∴ ⑤
⑤
上述解方程的过程中,是否有错误?答:;如果有错误,则错在__________步。如果上述解方程有错误,请你给出正确的解题过程:
解下列方程组:
(1)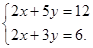
(2)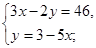
解下列方程:
(1) 4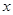 +3=2(
+3=2(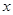 -1)+1
-1)+1
(2)
如图,正方形AOCB在平面直角坐标系xoy中,点O为原点,点B在反比例函数 (x>0)图象上,△BOC的面积为8.
(x>0)图象上,△BOC的面积为8.
(1)求反比例函数 的关系
的关系
(2)若动点E从A开始沿AB向B以每秒1个单位的速度运动,同时动点F从B开始沿BC向C以每秒2个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用S表示,求出S关于t的函数关系式?
(3)当运动时间为 秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
如图,直线 的解析表达式为
的解析表达式为 ,且
,且 与
与 轴交于点
轴交于点 ,直线
,直线 经过点
经过点 ,直线
,直线 ,
, 交于点
交于点 .
.
(1)求点 的坐标;
的坐标;
(2)求直线 的解析表达式;
的解析表达式;
(3)求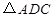 的面积;(4)在直线
的面积;(4)在直线 上存在异于点
上存在异于点 的另一点
的另一点 ,使得
,使得 与
与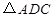 的面积相等,请直接写出点
的面积相等,请直接写出点 的坐标.
的坐标.