在光滑的水平面上，甲、乙两物质的质量分别为m1、m2，它们分别沿东西方向的一直线相向运动，其中甲物体以速度6m/s由西向东运动，乙物体以速度2m/s由东向西运动，碰撞后两物体都沿各自原运动方向的反方向运动，速度大小都是4m/s求：
①甲、乙两物体质量之比；
②通过计算说明这次碰撞是弹性碰撞还是非弹性碰撞。
如图所示为质谱仪的原理图，A为粒子加速器，电压为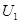
;B为速度选择器，磁场与电场正交，磁感应强度为
，板间距离为d；C为偏转分离器，磁感应强度为
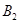，今有一质量为m、电荷量为q的正离子经过加速后，恰好通过速度选择器，进入分离器后做半径为R的匀速圆周运动，求：
（1）粒子的速度v
（2）速度选择器的电压
（3）粒子在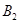磁场中做匀速圆周运动的半径R
光滑水平桌面上方存在垂直桌面向上范围足够大的匀强磁场，虚线框abcd内存在平行于桌面的匀强电场，如图所示，一带电小球从d处静止开始运动到b处时的速度方向与电场边界平行，通过磁场作用又回到d点，已知bc=2ab=2L，磁感应强度为B，小球的质量为m，电荷量为q，试分析求解
（1）小球的带电性质从d到b的运动性质
（2）小球子磁场中运动速度大小
（3）在电场中达到b位置的曲率半径
如图所示，风洞实验室中能模拟产生恒定向右的风力，质量m=100g的小球穿在长L=1.2m的直杆上并置于实验室中，球与杆间的动摩擦因数为0.5，当杆竖直固定放置时，小球恰好能匀速下滑，保持风力不变，改变固定杆与竖直线的夹角，将小球从O点静止释放，g取
，
。
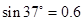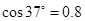，求
（1）当
时，小球离开杆时的速度大小
（2）改变杆与竖直线的夹角
，使球下滑过程中与杆之间的摩擦力为0，求此时的正切值
如图所示，水平放置的圆盘边缘C点有一个小洞，圆盘半径R=1m，在圆盘直径CD的正上方，与CD平行放置一条长为R的水平滑道AB，滑道右端B与圆盘圆心O在同一竖直线上，且B点距离圆盘圆心的竖直高度h=1.25m，在滑道右端静止放置质量m=2kg的物块（可视为质点），小球与滑道间的动摩擦因数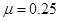
，现使小球以某一水平向左的初速度运动，同时圆盘从图示位置以图中所示的角速度
绕通过圆心O的竖直轴匀速转动，最终小球恰好落入圆盘边缘的小洞内，重力加速度取
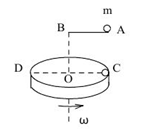
（1）小球运动的初速度
的大小
（2）圆盘运动角速度的值
某科研单位设计了一空间飞行器，飞行器从地面起飞时，发动机提供的动力方向与水平方向夹角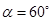
，使飞行器恰恰与水平方向成
角的直线斜向右上方由静止开始匀加速飞行，经时间t后，将动力的方向沿逆时针旋转60°同时适当调节其大小，使飞行器依然可以沿原方向匀减速飞行，飞行器所受空气阻力不计，下列说法中正确的是（）
| A．加速时动力的大小等于mg |
B．加速与减速时的加速度大小之比为 |
C．加速与减速过程发生的位移大小之比为 |
| D．减速飞行时间t后速度为零 |