(1)由数字0,1,2,3,4,5组成没有重复数字的六位数,其中个位数字小于十位数字的共有多少个?
(2)某高校从某系的10名优秀毕业生中选4人分别到西部四城市参加中国西部经济开发建设,其中甲同学不到银川,乙不到西宁,共有多少种不同派遣方案?
(3)将4个相同的白球、5个相同的黑球、6个相同的红球放入4各不同的盒子中的3个中,使得有一个空盒且其他盒子中球的颜色齐全的不同放法有多少种?
(本小题满分15分)已知点P(4,4),圆C: 与椭圆E:
与椭圆E: 有一个公共点A(3,1),F1.F2分别
有一个公共点A(3,1),F1.F2分别 是椭圆的左.右焦点,直线PF1与圆C相切.
是椭圆的左.右焦点,直线PF1与圆C相切.
(1)求m的值与椭圆E的方程;
(2)设Q为椭圆E上的一个动点,求 的范围.
的范围.
本小题满分14分)如图,四棱锥E—ABCD中,ABCD是矩形,平面EAB 平面ABCD,AE=EB=BC=2,F为CE上的点,
平面ABCD,AE=EB=BC=2,F为CE上的点,
且BF 平面ACE.
平面ACE.
(1)求证:AE BE;
BE;
(2)求三棱锥D—AEC的体积;
(3)求二面角A—CD—E的余弦值.
(本小题满分14分)
已知数列 中,
中, ,
, ,其前
,其前 项和
项和 满足
满足 ,令
,令 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求证:
,求证: (
( ).
).
(本小题满分14分)
在△ABC中,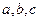 分别为角A、B、C的对边,
分别为角A、B、C的对边, 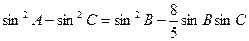 ,
, ="3," △ABC的面积为6,D为△ABC
="3," △ABC的面积为6,D为△ABC
内任一点,点D到三边距离之和为d。
(1)角A的正弦值;⑵求边b、c;⑶求d的取值范围
(本小题满分1 5分)
5分)
如图所示,已知直线 的斜率为
的斜率为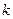 且过点
且过点 ,抛物线
,抛物线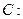
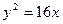 , 直线与抛物线
, 直线与抛物线 有两个不同的交点,
有两个不同的交点,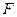 是抛物线的焦点,点
是抛物线的焦点,点 为抛物线内一定点,点
为抛物线内一定点,点 为抛物线上一动点.
为抛物线上一动点.
(1)求 的最小值;
的最小值;
(2)求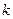 的取值范围;
的取值范围;
(3)若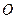 为坐标原点,问是否存在点
为坐标原点,问是否存在点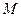 ,使过点
,使过点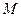 的动直线与抛物线交于
的动直线与抛物线交于 两点,且以
两点,且以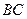 为直径的圆恰过坐标原点, 若存在,求出动点
为直径的圆恰过坐标原点, 若存在,求出动点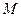 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.