由下面四个图形中的点数分别给出了四个数列的前四项,将每个图形的层数增加可得到这四个数列的后继项.按图中多边形的边数依次称这些数列为“三角形数列”、“四边形数列”
，将构图边数增加到
可得到“边形数列”，记它的第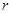
项为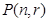
，
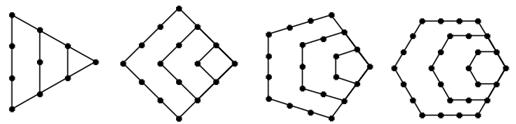
1，3，6，10 1，4，9，16 1，5，12，22 1，6，15，28
（1） 求使得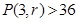
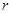的最小的取值；
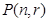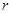（2） 试推导关于、的解析式；
( 3) 是否存在这样的“边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
(本小题满分12分)
一圆与
轴相切，圆心在直线
上，在
上截得的弦长为
，
求圆的方程。
已知函数
（Ⅰ）求
的值；
（Ⅱ）求
的最大值和最小值．
(14分)设
是椭圆
的两点，
，
，且
，椭圆离心率
，短轴长为2，O为坐标原点。
(1) 求椭圆方程；
(2) 若存在斜率为
的直线AB过椭圆的焦点
（
为半焦距），求的值；
(3) 试问
的面积是否为定值？若是，求出该定值；若不是，
说明理由。
(13分)已知数列{
}的前n项和Sn＝－－
＋2（n为正整数）．
（1）令
＝
，求证数列{}是等差数列，并求数列{}的通项公式；
（2）令
＝
,若Tn＝c1＋c2＋…＋cn, 求Tn。
(12分) 设
，
．
（1）求
在
上的值域；
（2）若对于任意
，总存在
，使得
成立，求
的取值范围．