计算：（1）（2）-优题课

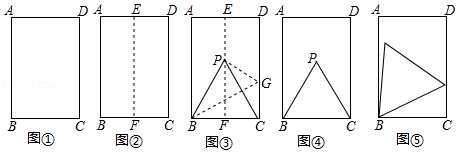
热气球的探测器显示，从热气球 $A$ 看一栋楼顶部 $B$ 的仰角 $α$ 为 $45 °$ ，看这栋楼底部 $C$ 的俯角 $β$ 为 $60 °$ ，热气球与楼的水平距离为 $100 m$ ，求这栋楼的高度（结果保留根号）．

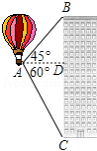
某学校为了解学生的课外阅读情况，随机抽取了50名学生，并统计他们平均每天的课外阅读时间 $t$ （单位： $\min$ ），然后利用所得数据绘制成如图不完整的统计图表．

课外阅读时间频数分布表

请根据图表中提供的信息回答下列问题：

（1） $a =$ 　　， $b =$ 　　；

（2）将频数分布直方图补充完整；

（3）若全校有900名学生，估计该校有多少学生平均每天的课外阅读时间不少于 $50 \min$ ？

先化简，再求值： $(m + 2 - \frac{5}{m - 2}) \cdot \frac{2 m - 4}{3 - m}$ ，其中 $m = - \frac{1}{2}$ ．

（1）计算： $| - 4 | - {(- 2)}^{2} + \sqrt{9} - {(\frac{1}{2})}^{0}$

（2）解不等式组 $\{\begin{matrix} 3 x - x ⩾ 2 \\ \frac{1 + 2 x}{3} > x - 1 \end{matrix}$ ．

折纸的思考．

（操作体验）

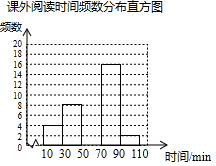
用一张矩形纸片折等边三角形．

第一步，对折矩形纸片 $ABCD (AB > BC)$ （图①），使 $AB$ 与 $DC$ 重合，得到折痕 $EF$ ，把纸片展平（图②）．

第二步，如图③，再一次折叠纸片，使点 $C$ 落在 $EF$ 上的 $P$ 处，并使折痕经过点 $B$ ，得到折痕 $BG$ ，折出 $PB$ 、 $PC$ ，得到 $ΔPBC$ ．

（1）说明 $ΔPBC$ 是等边三角形．

（数学思考）

（2）如图④，小明画出了图③的矩形 $ABCD$ 和等边三角形 $PBC$ ．他发现，在矩形 $ABCD$ 中把 $ΔPBC$ 经过图形变化，可以得到图⑤中的更大的等边三角形，请描述图形变化的过程．

（3）已知矩形一边长为 $3 cm$ ，另一边长为 $acm$ ，对于每一个确定的 $a$ 的值，在矩形中都能画出最大的等边三角形，请画出不同情形的示意图，并写出对应的 $a$ 的取值范围．

（问题解决）

（4）用一张正方形铁片剪一个直角边长分别为 $4 cm$ 和 $1 cm$ 的直角三角形铁片，所需正方形铁片的边长的最小值为　　 $cm$ ．