计算: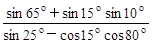
(本小题满分10分) 选修4—1:几何证明选讲.
已知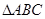 中,
中,  ,以点
,以点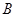 为圆心,以
为圆心,以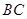 为半径的圆分别交
为半径的圆分别交 ,
,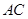 于两
于两 ,
,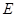 两点,且
两点,且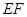 为该圆的直径.
为该圆的直径.
(1)求证:  ;
;
(2)若 .求
.求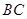 的长.
的长.
(本小题满分12分)
已知函数 .
.
(1)判断函数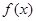 的单调性;
的单调性;
(2)若 ,当
,当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数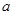 的取值范围.
的取值范围.
(本小题满分12分)
设点 ,
,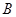 的坐标分别为
的坐标分别为 ,
, ,直线
,直线 ,
, 相交于点
相交于点 ,且它们的斜率之积是
,且它们的斜率之积是 .
.
(1)求点 的轨迹
的轨迹 的方程;
的方程;
(2) ,
, ,
, 为曲线
为曲线 上的三个动点,
上的三个动点,  在第一象限,
在第一象限,  ,
, 关于原点对称,且
关于原点对称,且 ,问
,问 的面积是否存在最小值?若存在,求出此时
的面积是否存在最小值?若存在,求出此时 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
(本小题满分12分)
如图,在三棱柱 中,
中, 平面
平面 ,
, ,
,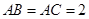 ,
, .
.
(1)过 的截面交
的截面交 于
于 点,若
点,若 为等边三角形,求出点
为等边三角形,求出点 的位置;
的位置;
(2)在(1)条件下,求平面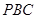 与平面
与平面 所成二面角的大小.
所成二面角的大小.
(本小题满分12分)
为了调查某高中学生每天的睡眠时间,现随机对20名男生和20名女生进行问卷调查,结果如下:
女生:
男生:
(1)从这20名男生中随机选出3人,求恰有一人睡眠时间不足7小时的概率;
(2)完成下面2×2列联表,并回答是否有90%的把握认为“睡眠时间与性别有关”?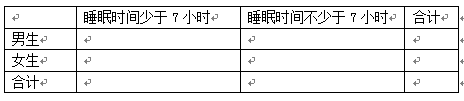
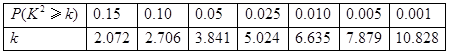
(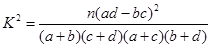 ,其中
,其中 )
)