小军的爸爸早晨从家骑自行车送小军去学校上学,他们的速度是12千米/时,用了0.5小时到达学校;放学时,让小军坐汽车,汽车的速度为V千米/时.
(1)写出t与V之间的函数关系式;
(2)如果小军要在10分钟内回到家,那么汽车的速度至少为多少?
(11·佛山)阅读材料
我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物;
比如我们通过学习两类特殊的四边形,即平行四边形和梯形(继续学习它们的特殊类型如矩形、等腰梯形等)来逐步认识四边形;
我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识;
请解决以下问题:
如图,我们把满足AB=CD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”;
(1)写出筝形的两个性质(定义除外);
(2)写出筝形的两个判定方法(定义除外),并选出一个进行证明;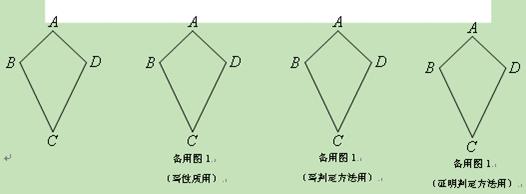
(11·佛山)商场对某种商品进行市场调查,1至6月份该种商品的销售情况如下:
①销售成本p(元/千克)与销售月份x的关系如图所示:
③销售量m(千克)与销售月份x满足m=100x+20 0;
0;
试解决以下问题:
(1)根据图形,求p与x之间的函数关系式;
(2)求该种商品每月的销售利润y(元)与销售月份x的函数关系式,并求出哪个月的
销售利润最大?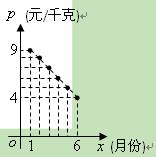
(11·佛山)现在初中课本里所学习的概率计算问题只有以下类型:
第一类是可以列举有限个等可能发生的结果的概率计算问题(一步试验直接列举,两步以上的试验可以借助树状图或表格列举),比如掷一枚均匀硬币的试验;
第二类是用试验或者模拟试验的数据计算频率,并用频率估计概率的概率计算问题,比如掷图钉的试验;
解决概率计算问题,可以直接利用模型,也可以转化后再利用模型;
请解决以下问题
(1)如图,类似课本的一个寻宝游戏,若宝物随机藏在某一块砖下(图中每一块砖除颜色外完全相同),则宝物藏在阴影砖下的概率是多少 ?
?
(2)在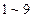 中随机选取3个整数,若以这3个整数为边长构成三角形的情况如下表:
中随机选取3个整数,若以这3个整数为边长构成三角形的情况如下表:
请你根据表中数据,估计构成钝角三角形的概率是多少?(精确到百分位)
(11·佛山)如图,一张纸上有线段AB;
(1)请用尺规作图,作出线段AB的垂直平分线(保留作图痕迹,不写作法和证明);
(2)若不用尺规作图,你还有其它作法吗?请说明作法(不作图);
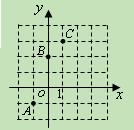
(11·佛山)如图,已知二次函数y=ax2+bx+c的图像经过A(-1,-1)、B(0,2)、C(1,3);
(1)求二次函数的解析式;
( 2)画出二次函数的图像;
2)画出二次函数的图像;