如图是一个路障的纵截面和汽车越过路障时的底盘示意图，O1、O2分别是车轮的轴心，M是线段O1O2的中点（轴心距的中点），两车轮的半径相等．经验告诉人们，只要中点M不被P点托住（俗称托底盘，对汽车很有危害！），线段O1O2上的其它点就不会被P点托住，汽车就可顺利通过．否则，就要通过其他方式通过．（1）若某种汽车的车轮半径为50cm, 轴心距O1O2为400cm. 通过计算说明,当∠APB等于多少度时，汽车恰好能通过斜坡？（精确到0.1，参考数据sin14.48º≈0.25，cos14.48º
≈0.97）（2）当∠APB=120°时，通过计算说明要使汽车安全通过，车轮半径与轴心距O1O2的比应符合什么条件？．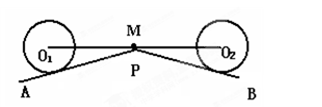
请根据图中提供的信息,回答下列问题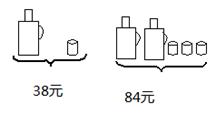
（1）一个暖瓶与一个水杯分别是多少元?
（2）甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定： 这两种商品都打九折；乙商场规定：买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯，请问选择哪家商场购买更合算，并说明理由.
已知A、B两地相距120km，乙的速度比甲每小时快1km，甲先从A地出发2小时后，乙从B地出发，与甲相向而行经过10小时后相遇，求甲、乙的速度各是多少？
如图直线AB、CD相交于点O，过点O作两条射线OM、ON，且∠AOM=∠CON=90°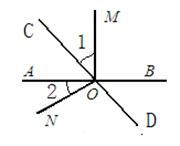
①若OC平分∠AOM，求∠AOD的度数.
②若∠1＝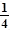
∠BOC，求∠AOC和∠MOD.
已知线段AB=16cm,C是线段AB上的一点,且AC=10cm,D为AC的中点,E是BC的中点，求线段DE的长
当x为多少时，x－
的值与7－
的值相等.