某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
计算:
已知:如图①,在 中,
中, ,
, ,
, ,点
,点 由
由 出发沿
出发沿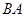 方向向点
方向向点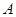 匀速运动,速度为1cm/s;点
匀速运动,速度为1cm/s;点 由
由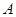 出发沿
出发沿 方向向点
方向向点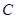 匀速运动,速度为2cm/s;连接
匀速运动,速度为2cm/s;连接 .若设运动的时间为
.若设运动的时间为 (
(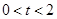 ),解答下列问题:
),解答下列问题:
(1)当 为何值时,
为何值时, ?
?
(2)设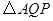 的面积为
的面积为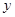 (
( ),求
),求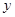 与
与 之间的函数关系式;
之间的函数关系式;
(3)是否存在某一时刻 ,使线段
,使线段 恰好把
恰好把 的周长和面积同时平分?若存在,求出此时
的周长和面积同时平分?若存在,求出此时 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(4)如图②,连接 ,并把
,并把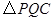 沿
沿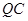 翻折,得到四边形
翻折,得到四边形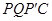 ,那么是否存在某一时刻
,那么是否存在某一时刻 ,使四边形
,使四边形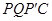 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
阅读材料:黑白双雄、纵横江湖;双剑合璧,天下无敌。这是武侠小说中常见的描述,其意是指两人合在一起,取长补短,威力无比。在二次根式中也有这种相辅相成的“对子”如: ,
, 与
与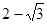 的积不含有根号,我们就说这两个式子互为有理化因式,其中一个是另一个的有理化因式。于是二次根式
的积不含有根号,我们就说这两个式子互为有理化因式,其中一个是另一个的有理化因式。于是二次根式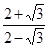 可以这样解:
可以这样解: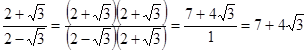 ,像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化。
,像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化。
解决问题:① 的有理化因式是_______________
的有理化因式是_______________
②计算: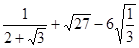
③计算: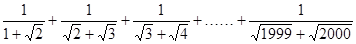
如图,梯形ABCD中,AD//BC,AB=CD,对角线AC、BD交于点O,AC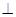 BD,E、F、G、H分别为AB、BC、CD、DA的中点.
BD,E、F、G、H分别为AB、BC、CD、DA的中点.
(1)求证:四边形EFGH为正方形;
(2)若AD=4,BC=6,求四边形EFGH的面积.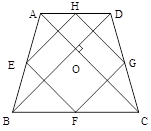
如图,DB∥AC,且DB= AC,E是AC的中点,
AC,E是AC的中点,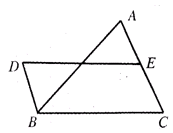
(1)求证:BC=DE;
(2)连结AD、BE,若要使四边形DBEA是矩形,则给△ABC添加一个什么条件,为什么?
(3)在(2)的条件下,若要使四边形DBEA是正方形,则∠C=0.