如图,在靠墙(墙长为18m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为35m,求鸡场的长y (m)与宽x (m)的函数关系式,并求自变量的取值范围。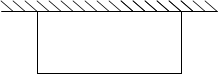
如图,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,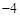 )两点。
)两点。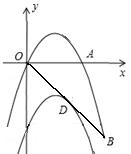
(1)求抛物线的解析式;
(2)将抛物线向下平移m个单位长度后,得到的抛物线与直线OB只有两个公共点D,求m的取值范围。
为了考察冰川融化的状况,一支科考队在某冰川上设定一个以大本营O为圆心,半径为4km 圆形考察区域,线段P1、P2是冰川的部分边界线(不考虑其它边界),当冰川融化时,边界线沿着与其垂直的方向朝考察区域平行移动.若经过n年,冰川的边界线P1P2移动的距离为s(km),并且s与n(n为正整数)的关系是 .以O为原点,建立如图所示的平面直角坐标系,其中P1、P2的坐标分别是(-4,9)、(-13,-3).
.以O为原点,建立如图所示的平面直角坐标系,其中P1、P2的坐标分别是(-4,9)、(-13,-3).
(1)求线段P1P2所在的直线对应的函数关系式;
(2)求冰川的边界线移动到考察区域所需要的最短时间.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D 出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.
(1)求NC,MC的长(用t的代数式表示)
(2)当t为何值时,四边形PCDQ构成平行四边形?
(3)当t为何值时,射线QN恰好将△ABC的面积平分?并判断此时△ABC的周长是否也被射线QN平分.
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为点C、D,连结CD、QC.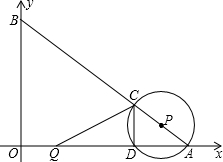
(1)当t为何值时,点Q与点D重合?
(2)当t为何值时,DQ=2AD?
(3)求线段QC所在直线与⊙P相切时t的值。
如图,在矩形ABCD中,AB=3,BC=4.动点P从点A出发沿AC向终点C运动,同时动点Q从点B出发沿BA向点A运动,到达A点后立刻以原来的速度沿AB返回.点P、Q运动速度均为每秒1个单位长度,当点P到达点C时停止运动,点Q也同时停止.连接PQ,设运动时间为t(t >0)秒.
(1)求线段AC的长度;
(2)当点Q从点B向点A运动时(未到达A点),求△APQ的面积S关于t的函数关系式,并写出t的取值范围;
(3)伴随着P、Q两点的运动,线段PQ的垂直平分线为l:
①当l经过点A时,射线QP交AD于点E,求AE的长;
②当l经过点B时,求t的值.